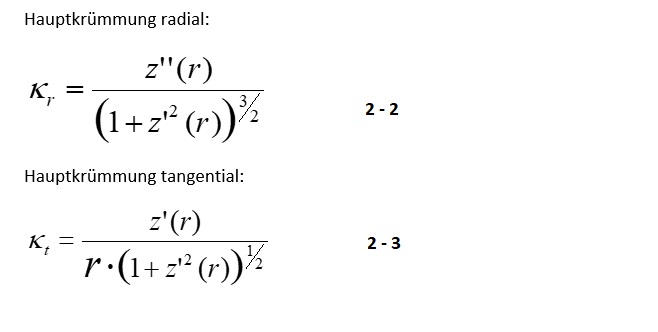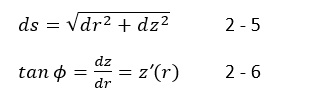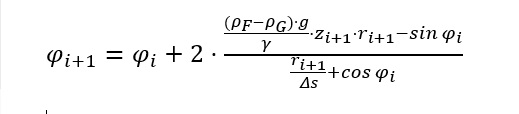Berechnung der Grenzflächenspannung aus Kraftmessungen an einem Ring
IMETER- Ringmethoden (YLP)
von T. Petzoldt und M. Breitwieser (2014-2024)
0 Aufbau 1 Kräftegleichgewicht am Fälchenelement 2 Differentialgleichung der Grenzflächenkontur 3 Numerische Berechnung der Grenzflächenkontur 4 Berechnung der Kraft 5 Messunsicherheit 6 Traditionelle Handhabung 7 Anmerkungen
Theorie der IMETER Ringmethoden M1/M2
Die Differentialgleichung zur Formulierung rotationssymmetrischer Grenzflächenkonturen wird hergeleitet, und als numerisches Verfahren angewendet.
0 Aufbau (Ring-Tensiometer)
Ein zylindrischer Behälter befindet sich mittig positioniert mit Flüssigkeit gefüllt auf einer vertikal beweglichen Plattform. Zentral über dem Behälter ist der Kraftmesser (Wägezelle), an dem über eine Aufhängung der Drahtring (ein Volltorus) befestigt wird (Abb. 1).Der Ring besteht aus einem von der Flüssigkeit gut benetzbaren Material wodurch der Kontaktwinkel zwischen Ring und Flüssigkeit näherungsweise Null beträgt.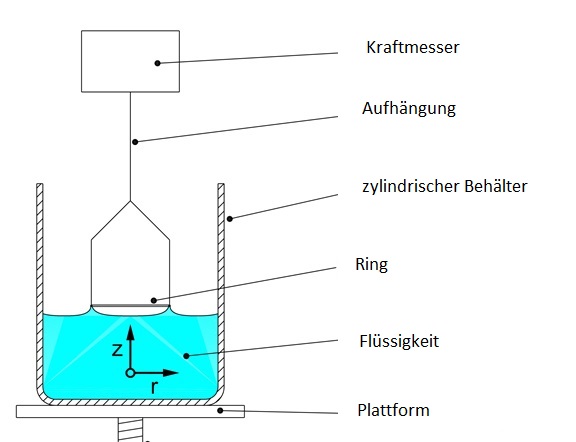 Abb.1 - schematischer Aufbau der "Ringmethode" (IMETER)
Abb.1 - schematischer Aufbau der "Ringmethode" (IMETER)
Zunächst wird die Plattform angehoben, bis der Ring vollständig in die Flüssigkeit eingetaucht ist und danach wieder langsam soweit abgesenkt, bis die Oberkante des Rings die Grenzfläche genau berührt. Dieser Zustand wird als Nullreferenz (Nullniveau) für die nachfolgenden Weg- und Kraftmessungen benötigt.
Formelzeichen: A Fläche [cm2]; α Winkel [rad]; d Differentialbezeichner; D Intervall / Differenz; g Ober- bzw. Grenzflächenspannung [mN/m]; F Kraft [mN]; j Konturwinkel [rad]; g Schwerebeschleunigung [m/sec2]; K Krümmung [1/mm]; p Druck [Pa]; r radiale Länge, Radius [mm]; R Hauptkrümmungsradius [mm]; r Dichte [g/cm3]; s Bogenlänge [mm]; Q Kontaktwinkel an der Gefäßwand [rad]; z axiale Länge, Höhe [mm].
1 Kräftegleichgewicht am Flächenelement
Für die Druckkraft, die auf ein sphärisch gekrümmtes, infinitesimales Flächenelement wirkt, gilt (Abb. 2):
dF = Δp·dA 1-1
Mit den beiden Radien in Richtung der Hauptkrümmungen kann für das Flächenelement geschrieben werden:
dA = R1·dφ1· R2dφ2 1-2
Entgegen der Druckkraft wirkt die aus der Grenzflächenspannung resultierende Kraft in Normalenrichtung zum Flächenelement wie folgt:
dF = γ· (R1·dφ1 · 2sin(dφ2/2) + R2·dφ2 · 2sin(dφ1/2)) 1-3
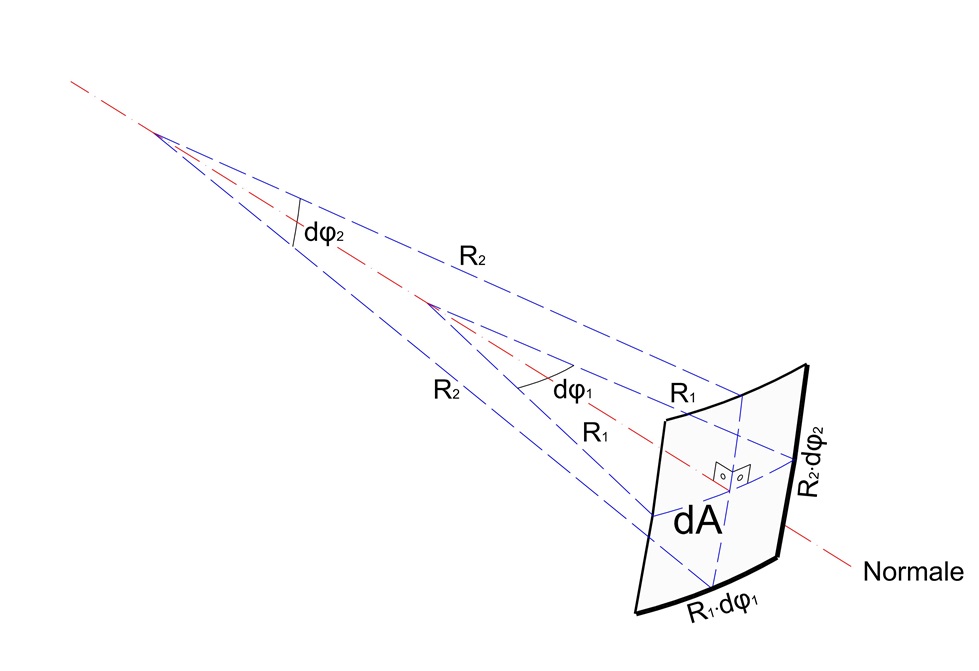 Abb. 2: Verbildlichung des grundlegenden Sachverhalts.
Abb. 2: Verbildlichung des grundlegenden Sachverhalts.
Mit der Vereinfachung für infinitesimal kleine Winkel
2sin(dφ/2) = dφ 1-4
können die beiden Kräfte ins Gleichgewicht gesetzt werden, wobei sich die Winkeltherme herauskürzen.
γ· (R1 + R2) = Δp·R1·R2 1-5
Die erhaltene direkte Beziehung zwischen Grenzflächenspannung und örtlicher Druckdifferenz wird mit den Krümmungen als Kehrwert des Krümmungsradius ausgedrückt.
K1 = 1/R1 ; K2 = 1/R2 1-6
γ·(K1 + K2) = Δp 1-7
Der Ausdruck 1-7 entspricht der Young-Laplace-Gleichung. Das Produkt beider Krümmungen in Hauptkrümmungsrichtung wird auch als Gauß’sche Krümmung bezeichnet.
2 Differentialgleichung der Grenzflächenkontur
Die hydrostatische Druckdifferenz zwischen den beiden Phasen ist eine Funktion der Steighöhe z.
Δp = (z - z0)·(ρF - ρG)·g 2-1
Die Höhenkoordinate z0, bei der die Druckdifferenz zu Null wird, soll fortan zu Null gesetzt werden (Nullniveau).
Die Kontur der Grenzfläche bei der Messung mit der Ringmethode ist rotationssymmetrisch. Daraus folgt, dass die Ausrichtung der beiden Hauptkrümmungen an jeder Position radial/tangential ist.
Durch Einsetzen der Gleichungen 2-1, 2-2 und 2-3 in Gleichung 1-7 erhält man als Differentialgleichung mit der radialen Konturfunktion z(r):
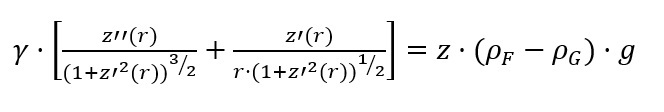 2 - 4
2 - 4
Obwohl Gleichung 2-4 relativ unhandlich erscheint, kann mit den geeigneten Umformungen und dem Setzen von Startbedingungen ein numerisches Ergebnis iterativ erzielt werden.
Für die Bogenlänge s und den Steigungswinkel φ der Konturfunktion gilt:
Damit wird aus den Krümmungen
Kr = dφ / ds 2 -7
Kt = sinφ / r 2 -8
und in Gleichung 2 -4 eingesetzt.
γ·(dφ/ds + sin(φ)/r) = z·(ρF - ρG)·g 2-9
3 Numerische Berechnung der Grenzflächenkontur
Zunächst wird Gleichung 2-9 wie folgt umgeformt:
dφ/ds = z·(ρF - ρG)·g/γ - sin(φ)/r 3 - 1
Die Wahl einer hinreichend kleinen Diskretisierungsschrittweite Δs stellt vom Rechenaufwand inzwischen kein Problem mehr dar.
Mit dem Festlegen zutreffender Anfangswerte rAnf, zAnf und φAnf ergibt sich der weitere Verlauf der Kontur aus den jeweils vorhergehenden Werten.
ri+1 = ri + Δs · cos φi 3 - 2
zi+1 = zi + Δs · sin φi 3 - 3
Zur Nachbildung der Lamellenkontur bei Ringauszug (Messaufbau Abb.1) wird zunächst die innere Grenzfläche berechnet. Ausgehend von der Symmetrieachse gilt:
Der Parameter zAnf wird dann solange variiert, bis die Konturkurve tangential innen an dem Drahtring anliegt (Abb. 3).
Die Anfangswerte für die äußere Grenzfläche ergeben sich aus der Randbedingung, dass die Konturkurve tangential außen am Drahtring anliegen muss. Dabei wird φAnf zum Iterationsparameter wodurch sich mit der Randbedingung rAnf und zAnf ergeben. Durch die Iteration wird dann φAnf so bestimmt, dass die Konturkurve die Behälterwand mit dem vorgegebenen Winkel schneidet (Abb. 3).
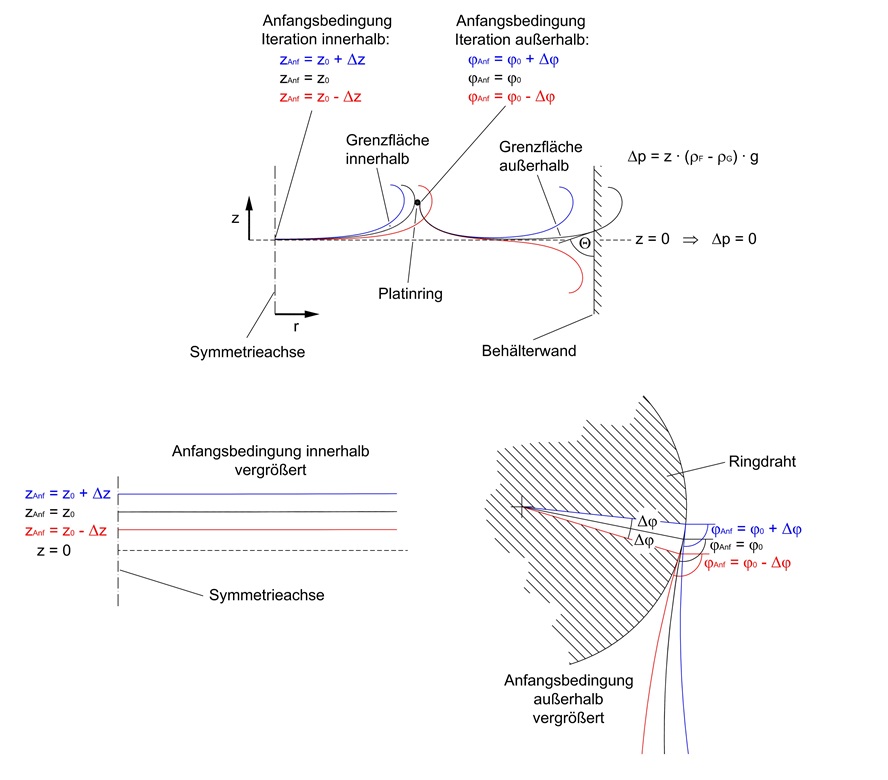 Abb.3: Skizzen zur Beschreibung des mathematischen Vorgehen.
Abb.3: Skizzen zur Beschreibung des mathematischen Vorgehen.
4 Berechnung der Kraft am Ring
MIt der bekannten Kontur der Grenzfläche wird die resultierende Gesamtkraft am Ring bestimmt. Diese summiert sich aus drei Komponenten (Abb. 4).
Fγa = γ·2π· ra · cos αa 4 - 2
Fp Integration der örtlichen Druckdifferenz über den Ringumfang und das benetzte Drahtsegment. 4 - 3
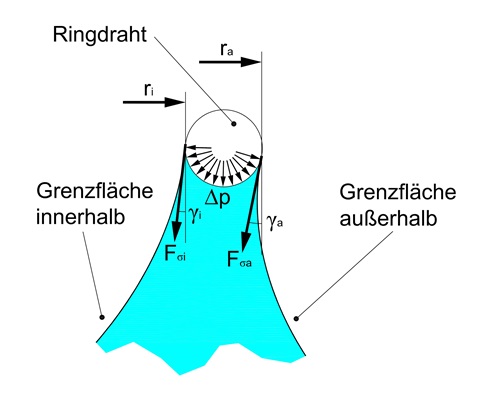 Abb.4: (...) Konstruktion der Benetzungkraft, die bei Kontaktwinkel 0 zwischen Draht und Fluid tangential an der Ringoberfläche angreift.
Abb.4: (...) Konstruktion der Benetzungkraft, die bei Kontaktwinkel 0 zwischen Draht und Fluid tangential an der Ringoberfläche angreift.
Bemerkenswert, es resultiert für die praktische Messung, dass kleine Auslenkungen aus der rotationssymmetrischen Anordnung kraftbedingt wieder in Koaxialität gezwungen werden (Ringmittelpunkt = Gefäßmittelpunkt). Der Aufbau in typischen Proportionen korrigiert einen sonst nicht-auszuschließenden Mittelpunktsfehler einfach selbst. Übrigens verdeutlicht diese Skizze, dass eine Variation des Ringmaterials, wobei alle anderen Größen bekannt sind, die Kontaktwinkel- und mithin die Oberflächenenergiebestimmung diesen Materials fokussieren kann, so zum Goniometer wird und Feststoff-oberflächeneigenschaften in diese Theorie inkorporiert.
Abb. 5 zeigt beispielhaft einen mit dem beschriebenen Verfahren berechneten Weg-Kraft Verlauf (mit den Daten zu Beispiel ①).
 Abb.5: 'Wasser' - gemäß YLP berechneter Weg-Kraft-Verlauf unter Einsetzung der Daten von "Beispiel ① IDN°23836 (Abb. -1, Abb.0. Weitere Besprechung in Kapitel 7: zu "Beispiel ①").
Abb.5: 'Wasser' - gemäß YLP berechneter Weg-Kraft-Verlauf unter Einsetzung der Daten von "Beispiel ① IDN°23836 (Abb. -1, Abb.0. Weitere Besprechung in Kapitel 7: zu "Beispiel ①").
5 Messunsicherheit - Betrachtungen über die Empfindlichkeit der Eingangsgrößen
Eine Handreichung für wissenschaftliche Überprüfungen bietet das Dokument Beispiel ① Wasser_ID23836.pdf (ID23836_Wasser_std_YLP_extended.pdf). Darin finden sich Mess- und Simulationsdaten zusammen- und gegenübergestellt. Die Daten dieser Messung dienen in den nachfolgenden Diagrammen als Eingangsdaten der Berechnung. In Kapitel 7.1 wird Beispiel ② Wasser_ID23844.pdf besprochen, bei dem Flüssigkeitspegel- und der Gefäßrand-Kontaktwinkel zur Messung konstant gehalten werden zur (Halb-)Simulation einer unendlichen Behälteroberfläche. Die beiden Messungen in den Beispielen wurden zeitlich sehr kurz aufeinander folgend und mit den selben Geräten ausgeführt.
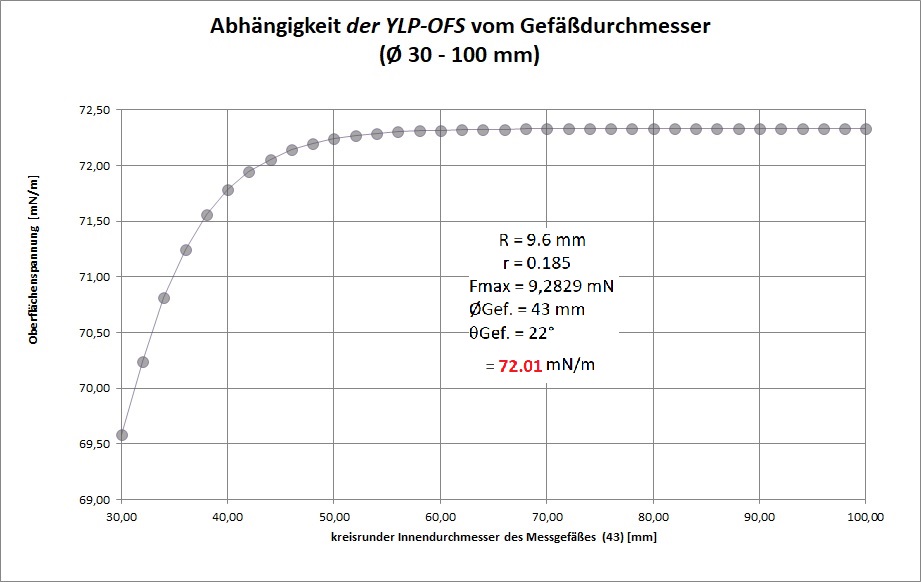
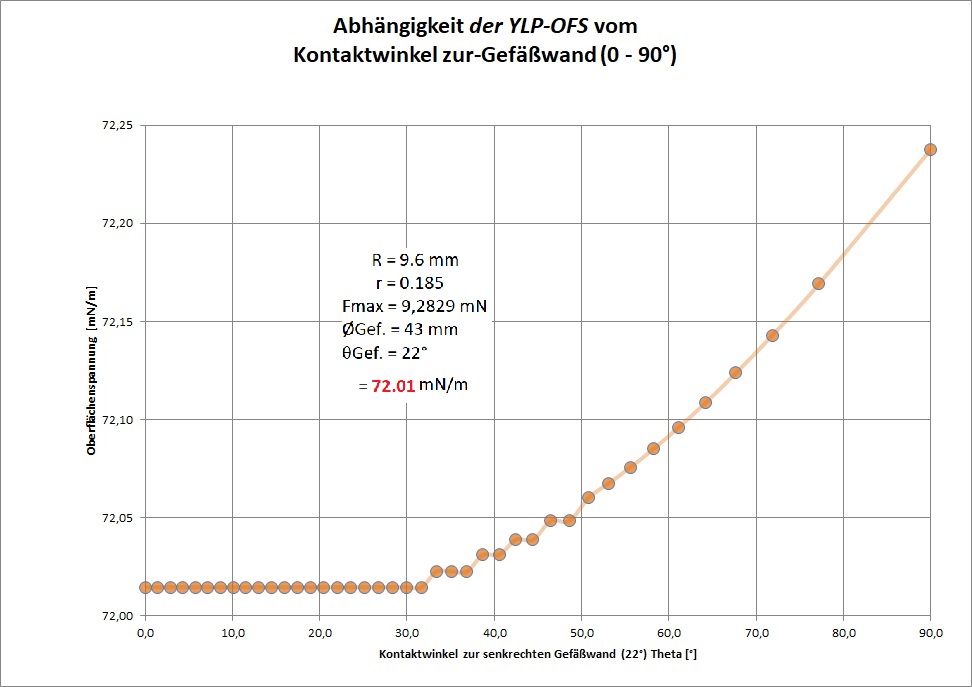
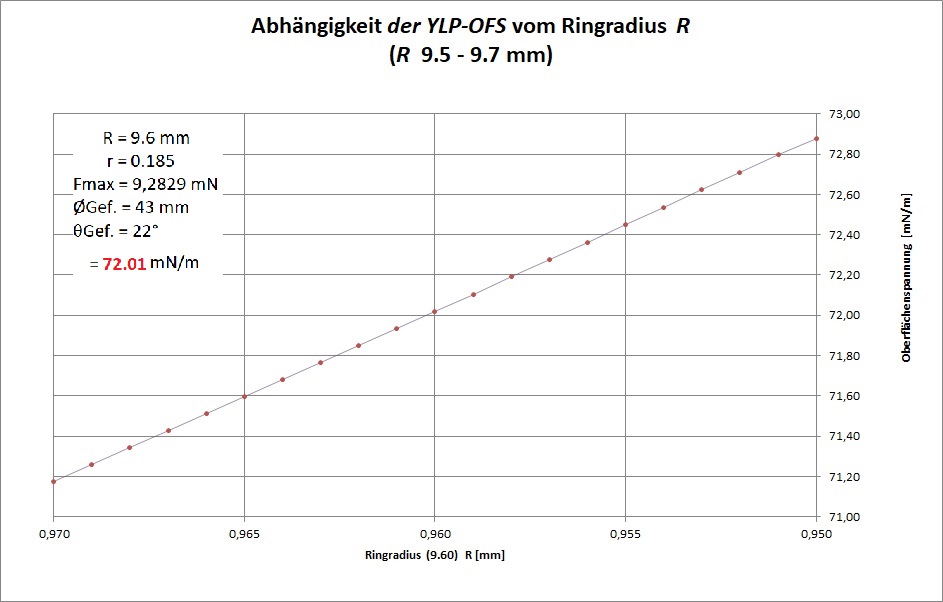
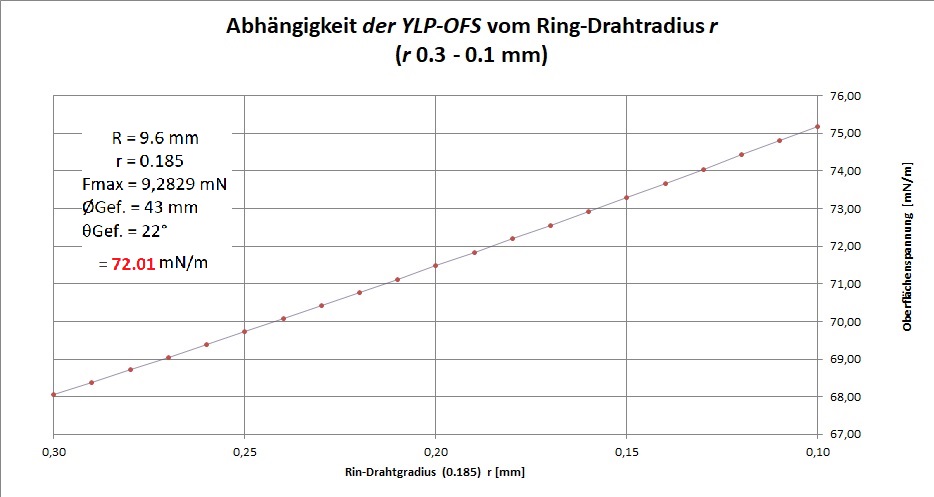
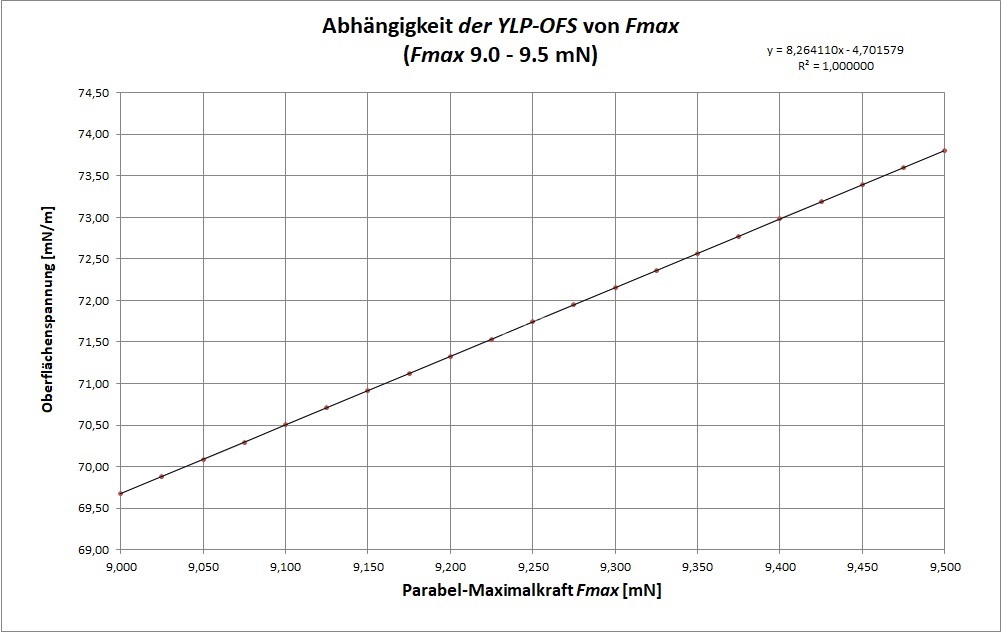
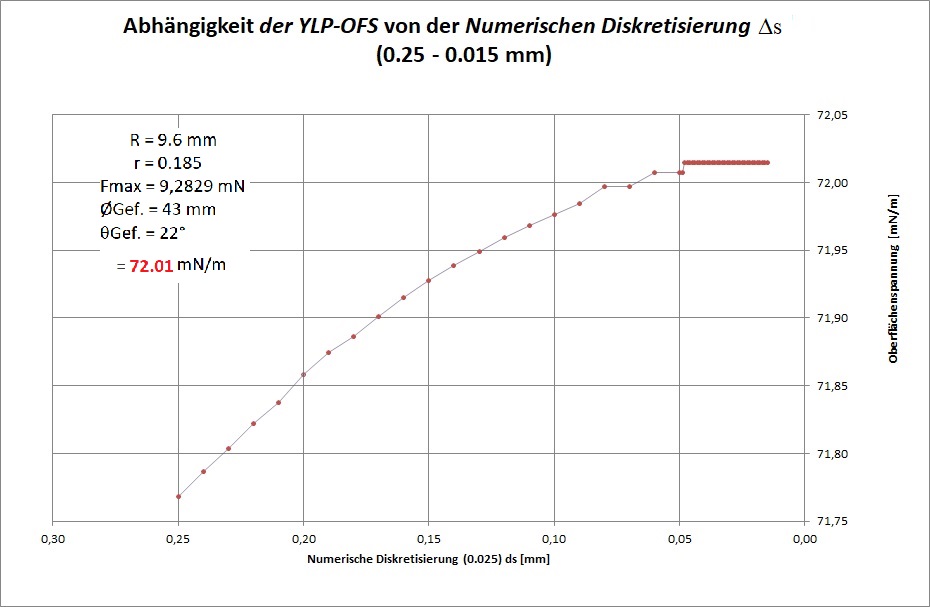
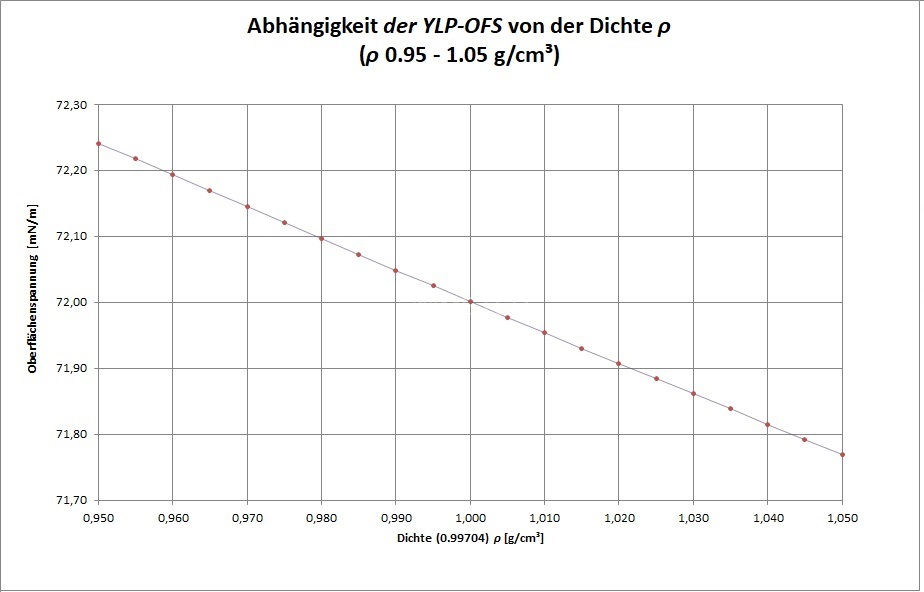
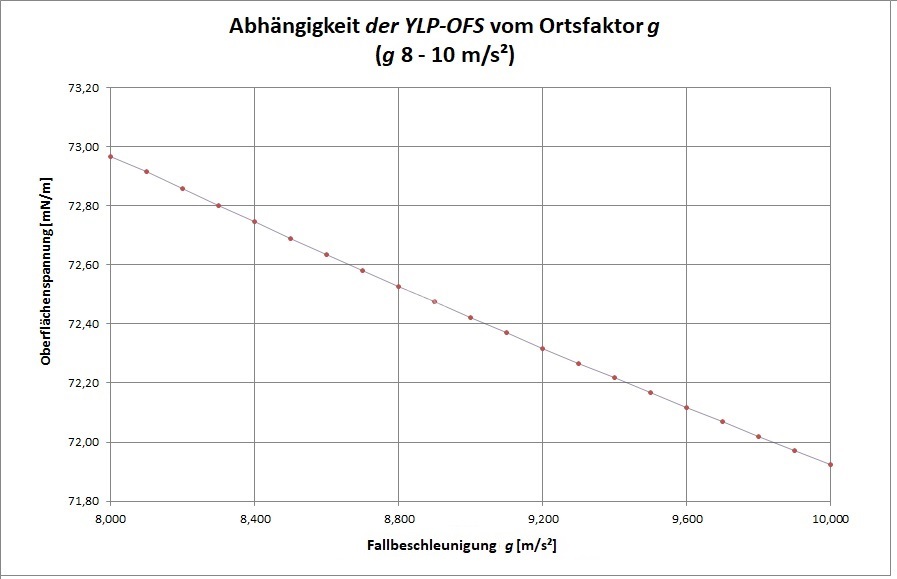
Zur Untersuchung der Einflußgrößen werden die Daten aus dem Dokument Beispiel ① Wasser_ID23836.pdf verwendet. Berechnet wurde überschlagsmäßig die Präzisionsmöglichkeit der anzugebenden Oberflächenspannung unter Variation aller möglichen Größen und sogar des Ortsfaktors (g). So offenbaren die folgenden Diagramme, welche Oberflächenspannung angezeigt würde, wenn im Parametersatz der Lösungsgleichungen die Größenwerte mutieren. Die Abhängigkeit bzw. Empfindlichkeit der berechneten Oberflächenspannung von den unterschiedlichen Eingangsgrößen sind hilfreich zum Verständnis und unabdingbar für eine Messunsicherheitsbetrachtung.
Außer bei Gefäßparametern (RGef, θ) stellen sich die untersuchten Abhängigkeiten als gut linear dar. Insofern dürfen Abweichungen durch Kalibrierung mittels Standardflüssigkeit legal und so wie bisher in einem einzigen Korrekturfaktor untergebracht werden. Beim kalibrierten Messaufbau (...) bestimmt alleine die Auflösung der Kraft-Messung über die anzugebende Präzission der Oberflächenspannung. Um sicher zu sein, sollte eine Kalibrierung im näheren Wertebereich der Proben liegen. Neben den bekannten Messmethoden Oberflächenwellen, schwingende Strahlen, kapillare Steighöhe und hängende Tropfen (vgl.⇒Methoden) kommt nun die IMETER Ringmethode als Referenzmethode in Betracht (wie hier begründet). So kann die Grenzflächenspannung zwischen undurchsichtigen Fluiden richtig gemessen werden und es kann beispielsweise der Übergang von statischer zu dynamischer Oberflächenspannung messtechnisch untersucht werden.Die IMETER-Methode stellt sich als wissenschaftlich kohärente Methode dar, die die Oberflächenspannung als das misst, was sie dem Wesen nach ist - eine Kraft.
Der Vergleich von ab initio Berechnungen mit Exprerimentaldaten kann Fehler oder Unbekanntes aufzeigen. Messung und Berechnung befinden sich soweit erkennbar in widerspruchsfreier Übereinstimmung. Verschiedene Falsifikationen unter Variaton der Flüssigkeit und Ringdimensionen ergaben ebenfalls keine Widersprüche zwischen Theorie und Praxis. So liegt messtechnisch offenbar ein geeignetes Modell vor, das es erlaubt, eine Materie-Eigenschaft mit hoher Präzission zu bestimmen..
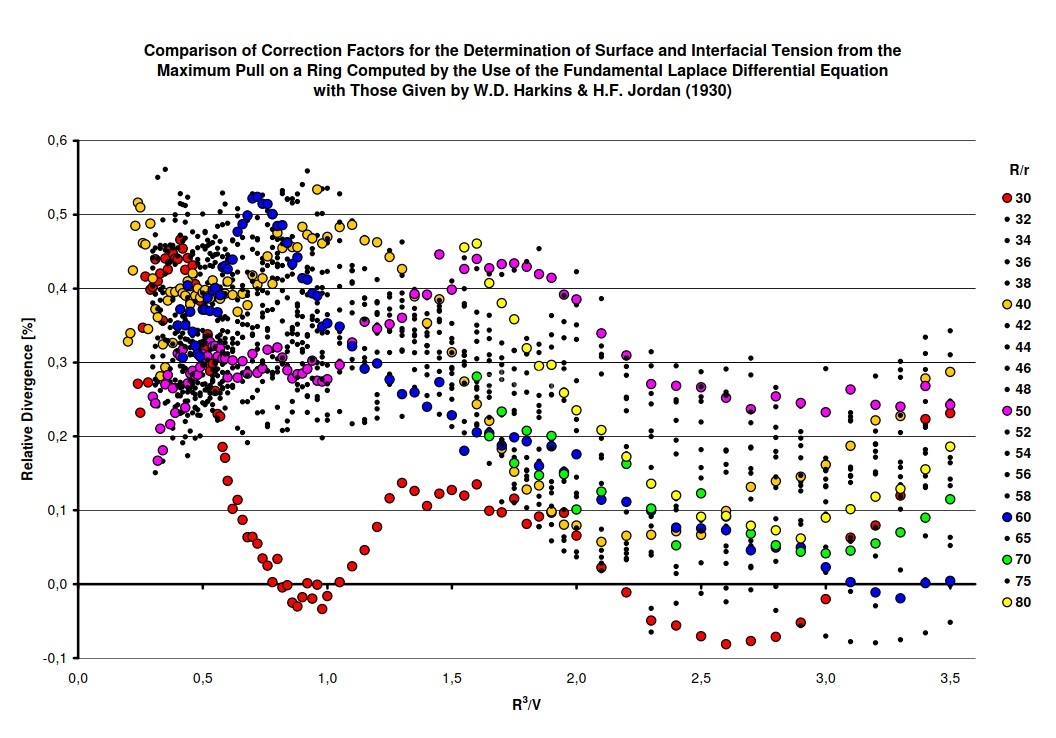
6 Verbesserung der traditionellen Handhabung
|
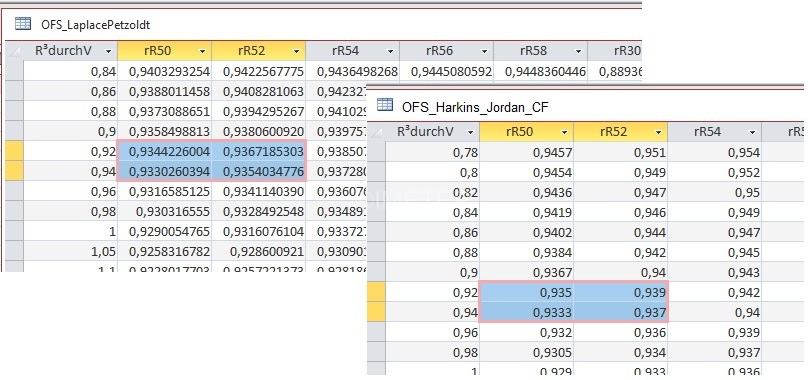
Wegen Rechengeschwindigkeit ('2025 immer noch) verwendet die IMETER-Software ebensolche Tabellen. Bei exotischen Kombinationen werden die Ergebnisse über die Differentialgleichung berechnet - und dies braucht je Kurve ein paar Sekunden. ⇒ PDF: YLP-Korrekturfaktorentafel (IMETER). Die PDF-Tabelle kann frei verwendet werden. Auch wenn man über kein IMETER-Gerät verfügt, kann die mutmaßlich richtigere und präzisere IMETER-Korrekturfaktorentafel bessere Ergebnisse auf anderen Vorrichtungen ermöglichen. Die wichtige Erkenntnis über den Einfluß der Gefäßgröße und Randbenetzung sollte dabei beherzigt werden. Zwar benetzen fast alle organischen Fluide, die typischerweise mit Tensiometern untersucht werden, Glasgefäße perfekt. Bei Flüssigkeiten mit hoher Oberflächenspannung (anorganische Stoffe) kann die notwendige Messgefäß-Benetzung den Einsatz von Spezielgefäßen erforderlich machen. |
7 Ableitungen, Anmerkungen und Nachträge zu IMETER Ringmethoden
7.1 Messung der Oberflächenspannung bei "unendlicher Oberfläche" bzw. der spezielle Einfluß der Gefäßwand
Messung, Simulation und Vergleich der statischen Oberflächenspannung bei unendlicher Oberfläche durch Konstanthaltung von Niveau und Kontaktwinkel und Simulationsrechung für große Oberflächen:
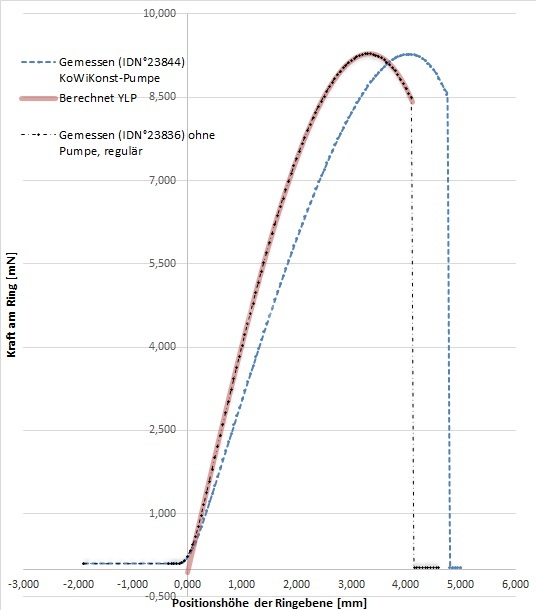 Abb.7.1.1: Messkurven zur Oberflächenspannung an Wasser. Messung mit und ohne Kontantwinkel-Konstanthalte-Verfahren und YLP-Berechnung mit RGef=21.5mm.
Abb.7.1.1: Messkurven zur Oberflächenspannung an Wasser. Messung mit und ohne Kontantwinkel-Konstanthalte-Verfahren und YLP-Berechnung mit RGef=21.5mm.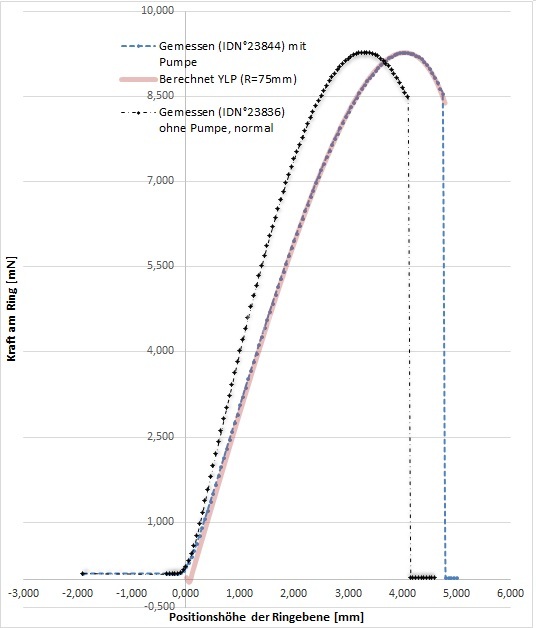 Abb.7.1.2: Messkurven zur Oberflächenspannung an Wasser. Messung mit und ohne Kontantwinkel-Konstanthalte-Verfahren und YLP-Berechnung mit RGef=75mm.
Abb.7.1.2: Messkurven zur Oberflächenspannung an Wasser. Messung mit und ohne Kontantwinkel-Konstanthalte-Verfahren und YLP-Berechnung mit RGef=75mm.
Abb.7.1.1 und .2 zeigen jeweils zwei nahezu deckungsgleiche Kurven, die den Kraft- Wegverlauf beim Herausziehen eines DeNoüy-Ringes aus einer Wasseroberfläche wiedergeben. Die durchgezogene rötliche Linie markiert jeweil den theoretisch berechneten Kraftverlauf, die schwarzen bzw. blauen Punkte repräsentieren Kraftmesswerte zweier physischer Messung. Die Kurve der blauen Punkte, zeigt eine im Vergleich eine deutlich höher ausgezogene Lamelle und gehört zum Prüffall der unendlich ausgedehnten Oberfläche (A→∞). Hierfür wurde nämlich der Pegel im Gefäß während des gesamten Messvorgangs konstant gehalten; als ob die Oberfläche unendlich ausgedeht wäre. Normalerweise sinkt der Flüssigkeitsspiegel indem am herausgezogenen Ring eine Flüssigkeitsmenge gehoben wird.
Die YLP-Rechnung zur simulierten Gefäßgröße RGef=75 mm nähert den Werteverlauf der physischen Messung an, deutet aber an, dass sich der berechnete Oberflächeneffekt vom Fall unendlicher Ausdehnung geringfügig unterscheidet (vgl. Abb.:7.1.2).
(IGemäß der dargelegten Theorie kann die unendliche Oberfläche mit YLP nicht berechnet werden; Ø150mm stellt eine Annäherung dar)
Im PDF-Dokument Beispiel ② Wasser_ID23844.pdf finden Sie die Dokumentation der Messung mit ausführlicher Aufarbeitung aller verfügbaren Daten. Dort ist auch das IMETER-Messprogramm abgedruckt, worin die Option der Pumpensteuerung zur Niveauregulierung beschrieben ist. Um eine unendlich ausgedehnte Oberfläche darzustellen bzw. für die physische Messung zu simulieren, wurde eine vom IMPro (=IMETER-Messprogramm) aus gesteuerte, µL-genau arbeitende Kolbenpumpe eingesetzt, um durch Zu- oder Abdosierung die hydrostatisch bewegten und gewogenen Volumen auszugleichen. Wie diese Technik im IMETER-Modulsystem funktioniert, ist auf der Seite "Kontaktwinkel-Konstanter-Verfahren" beschrieben. Im bereits referierten Dokument Beispiel ① Wasser_ID23836.pdf findet sich die gleiche Messung ohne Niveauautomatik dokumentiert.
Abb.7.1.3 zeigt zwei den Messungen entsprechende Profilkurven übereinander geplottet, die vom letzten Iterationsschritt vor dem Lamellenabriß stammen.
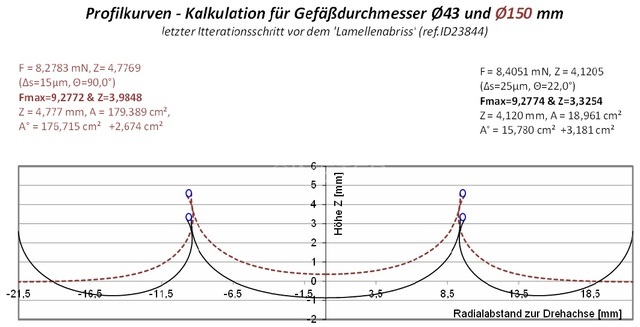 Abb. 7.1.3: Vergleich der Profilkurven mit und ohne Niveauautomatik. Das Diagramm zeigt die Profile kurz vor dem Lamellenabriss - also nach Überschreitung der Maxiamlkraft. Die Maximalkraft (Fmax) ist für beide Kalkulationen praktisch gleich und mit 9.2773 mN in der Messung ID23844 bestimmt und der Kalkulation vorgegeben. Die Messung ID23844 liefert mit YLP-OFS 71.97 mN/m den gleichen Wert wie das Ergebnis der Simulation mit dem tatsächlich eingesetzten Gefäß (Ø=43mm). Die Auszughöhe bis Fmax ist in der Messung (3.92mm) jedoch vergleichbar mit quasi 'unendlicher Oberfläche' {Ø150mm}.
Abb. 7.1.3: Vergleich der Profilkurven mit und ohne Niveauautomatik. Das Diagramm zeigt die Profile kurz vor dem Lamellenabriss - also nach Überschreitung der Maxiamlkraft. Die Maximalkraft (Fmax) ist für beide Kalkulationen praktisch gleich und mit 9.2773 mN in der Messung ID23844 bestimmt und der Kalkulation vorgegeben. Die Messung ID23844 liefert mit YLP-OFS 71.97 mN/m den gleichen Wert wie das Ergebnis der Simulation mit dem tatsächlich eingesetzten Gefäß (Ø=43mm). Die Auszughöhe bis Fmax ist in der Messung (3.92mm) jedoch vergleichbar mit quasi 'unendlicher Oberfläche' {Ø150mm}.
Zu konstatieren ist, dass die Bedeutung der Messkraft als Oberflächenspannung γ durch die Gefäßgröße wesentlich mitbestimmt wird.
Die Maximalkraft (Fmax) ist für beide Kalkulationen gleich und mit 9.2773 mN in der Messung ID23844 bestimmt und der Kalkulation vorgegeben. Die Bedeutung der Messkraft als Oberflächenspannung γ wird trotzdem durch die Gefäßgröße wesentlich modifiziert. So beträgt die Oberflächenspannung berechnet über die Differentialgleichung γØ43 = 71,968 bzw. γØ150 =72,297 mN/m. Die Berechnung für unendliche Oberfläche, also die YLP-Berechnung für ein Ø150mm-Gefäß, versagt also mit den unter Niveaukonstanz gemessenen Daten. Diese Daten ergeben (korrekte) 71.97 mN/m wenn in der Berechnung mit dem tatsächlich eingesetzten Gefäß (Ø=43mm) gemäß YLP kalkuliert wird. Gleichwohl die im Experiment bestimmte Ausziehhöhe zur Gefäßoberfläche ‚unendlich‘ (d.h. Ø=150mm) passt, wird maximale Kraft am Ring durch Gefäßwandbenetzung und den tatsächlichen Wandabstand reduziert.
Präzisionsmessungen sollten mit der Methode der Kontaktwinkel-Konstanthaltung bevorzugt durchgeführt werden, wenn rheologische Eigenschaften der zu messenden Flüssigkeit Kontaktwinkeleffekte hervorrufen können.
7.2 Verschiedene Ringgrößen mit/ohne Niveau- & Kontaktwinkelkonstanthaltung
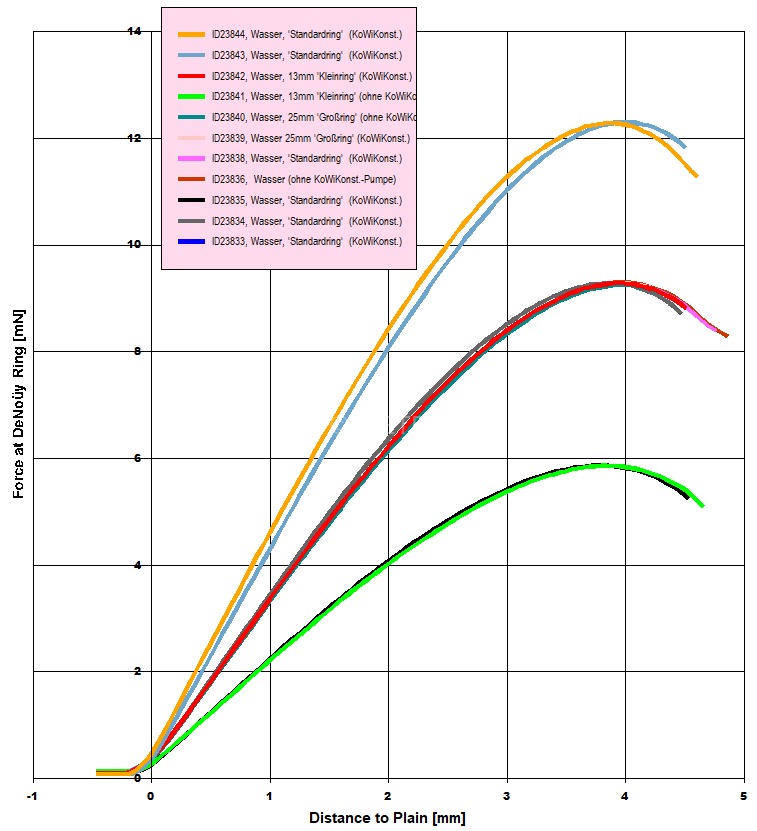 Abb.9.2.1: Wasser: Variation Ringradius und Variation Oberfläche (Ø 43mm gegen 'unendliche' Gefäßweite) - Messkurven zur Oberflächenspannung an Wasser, mit Ringen Ø13, 20, 25mm, mit/ohne "Kontaktwinkel-Konstanthalte-Verfahren".
Abb.9.2.1: Wasser: Variation Ringradius und Variation Oberfläche (Ø 43mm gegen 'unendliche' Gefäßweite) - Messkurven zur Oberflächenspannung an Wasser, mit Ringen Ø13, 20, 25mm, mit/ohne "Kontaktwinkel-Konstanthalte-Verfahren".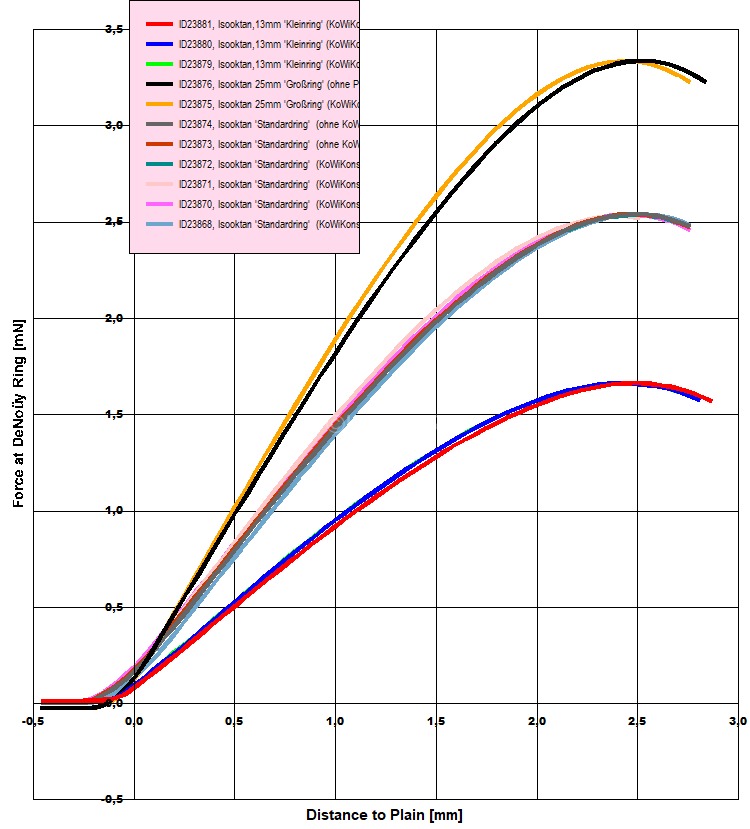 Abb.9.2.2:IsoOktan: Variation Ringradius und Variation Oberfläche (Ø 43mm gegen 'unendliche' Gefäßweite) - Messkurven zur Oberflächenspannung an 2,4,4-Trimethypentan, mit Ringen Ø13, 20, 25mm, mit/ohne "Kontaktwinkel-Konstanter")
Abb.9.2.2:IsoOktan: Variation Ringradius und Variation Oberfläche (Ø 43mm gegen 'unendliche' Gefäßweite) - Messkurven zur Oberflächenspannung an 2,4,4-Trimethypentan, mit Ringen Ø13, 20, 25mm, mit/ohne "Kontaktwinkel-Konstanter")
Die Diagramme zeigen Messkurven zur Oberflächenspannung mit Ringen der Radien 6.5, 9.6 und 12.5mm (Ø13, 20, 25mm). Dabei wurde abwechselnd auch das "KontaktwinkelKonstanter-Verfahren" eingesetzt. (Die IMETER-Software berechnet bei Gefäß-Durchmesser Angabe eine gleitende Niveauverschiebung über die Kraft am Ring. Bei Oberfläche ∞ berechnet die Software die Niveauveränderung von Null ein. Die Kurvenverläufe mit bzw. ohne Niveauregulierung weichen in ihrer Bogenform leicht von einander ab, was der Effekt des angepinnten Kontaktwinkel zur Gefäßwand sein dürfte. - Die Kurvenvergleiche sind allerdings wegen des Antastverfahrens für Nullniveaus im IMPro der Beispiele suboptimal konfiguriert gewesen!)
Ein Besonderer Umstand kann Richtung geben und eine Weiterentwicklung der Lösungsgleichung nach der (after-at-tangent) 'Nullstelle' zu ergänzen. In Abb. 7.2.1 zeigen zwei der mittleren Kurven (Standardring 20mm) viele Messpositionen, die über den Tangenzialberührpunkt hinaus führen. Die Lamelle ist nicht in Erwartungshöhe abgerissen sondern wurde beträchtlich weiter ausgezogen, wobei in diesem Kurvenabschnitt ein Wendepunkt erkennbar wird.