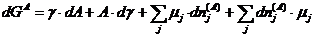1 Phänomen & Begriffe
Die Oberflächenspannung ist neben Dichte und Viskosität die dritte wichtige Eigenschaft von Flüssigkeiten. Die relative Größe des Wertes der Oberflächenspannung (γ) ist augenfällig: Etwas in eine Schale gegebenes Quecksilber gleitet in Form ziemlich perfekter Kügelchen am Gefäßboden herum; dabei würde  Ein Schwarm Stare: Es bildet sich näherungsweise eine Minimaloberfläche, weil kein Vogel gerne außen fliegt (insbesondere, wenn ein Falke jagt). - Bei Flüssigkeiten führt die gegenseitige Anziehung der Teilchen zum gleichen Phänomen. eigentlich die hohe Dichte - ein Liter davon wiegt immerhin rund 14 Kilogramm - jedes Tröpfchen flunderplatt drücken. Der Schwerkraft stemmt sich die Oberflächenspannung entgegen. Sie ist bei Quecksilber sehr groß (γ=484 mN/m). Ein Tropfen Öl (mit γ ~ 30-40mN/m) verhält sich bekanntermaßen anders: obwohl die Dichte viel geringer ist, zerfließen Öltröpfchen zu dünnen Filmen. Ursache der Ober- und Grenzflächenspannung ist die gegenseitige Anziehung der Teilchen die in flüssigem Metallen offenbar sehr hoch ist. Extrem beweglich, wie ohne Haut, wirken demgegenüber kleine Spannungen, wie sie als Grenzflächenspannungen von < 5 mN/m zwischen Benzin und Seifenwasser – nach sehr vorsichtigem überschichten – sichtbar werden können. Effekte der Grenzflächenspannung zu festen Stoffen kennt man im Übrigen aus der Anschauung: Öl in der Teflonpfanne lässt sich auf dieser Oberfläche nicht gut zu einem Film verteilen (spreiten), es hat den unbedingten Drang wieder zusammenzufließen, um so möglichst wenig der Teflonfläche zu bedecken (benetzen). Andererseits kann man Stahlpfannen mühelos mit einem Ölfilm bestreichen. Während im ersten Fall Teflon eine geringe Oberflächenenergie hat, die geringer als die des Öls ist, ist die des Stahls größer. Wie die Begriffe "Ober- bzw. Grenzflächenenergie" schon andeuteten, sind Energien am Werk – und diese suchen sich zu minimieren. Der Energieinhalt des Systems ist minimal, wenn das Öl die Metalloberfläche bedeckt bzw. die des Teflons eben nicht. Der Braten in einer teflonbeschichteten oder unbeschichteten Pfanne gibt im mehr oder weniger festgeklebten Resultat einen fühlbaren Zusammenhang mit der Adhäsion wieder.
Ein Schwarm Stare: Es bildet sich näherungsweise eine Minimaloberfläche, weil kein Vogel gerne außen fliegt (insbesondere, wenn ein Falke jagt). - Bei Flüssigkeiten führt die gegenseitige Anziehung der Teilchen zum gleichen Phänomen. eigentlich die hohe Dichte - ein Liter davon wiegt immerhin rund 14 Kilogramm - jedes Tröpfchen flunderplatt drücken. Der Schwerkraft stemmt sich die Oberflächenspannung entgegen. Sie ist bei Quecksilber sehr groß (γ=484 mN/m). Ein Tropfen Öl (mit γ ~ 30-40mN/m) verhält sich bekanntermaßen anders: obwohl die Dichte viel geringer ist, zerfließen Öltröpfchen zu dünnen Filmen. Ursache der Ober- und Grenzflächenspannung ist die gegenseitige Anziehung der Teilchen die in flüssigem Metallen offenbar sehr hoch ist. Extrem beweglich, wie ohne Haut, wirken demgegenüber kleine Spannungen, wie sie als Grenzflächenspannungen von < 5 mN/m zwischen Benzin und Seifenwasser – nach sehr vorsichtigem überschichten – sichtbar werden können. Effekte der Grenzflächenspannung zu festen Stoffen kennt man im Übrigen aus der Anschauung: Öl in der Teflonpfanne lässt sich auf dieser Oberfläche nicht gut zu einem Film verteilen (spreiten), es hat den unbedingten Drang wieder zusammenzufließen, um so möglichst wenig der Teflonfläche zu bedecken (benetzen). Andererseits kann man Stahlpfannen mühelos mit einem Ölfilm bestreichen. Während im ersten Fall Teflon eine geringe Oberflächenenergie hat, die geringer als die des Öls ist, ist die des Stahls größer. Wie die Begriffe "Ober- bzw. Grenzflächenenergie" schon andeuteten, sind Energien am Werk – und diese suchen sich zu minimieren. Der Energieinhalt des Systems ist minimal, wenn das Öl die Metalloberfläche bedeckt bzw. die des Teflons eben nicht. Der Braten in einer teflonbeschichteten oder unbeschichteten Pfanne gibt im mehr oder weniger festgeklebten Resultat einen fühlbaren Zusammenhang mit der Adhäsion wieder.
1.1 Herkunft von Ober- und Grenzflächenspannung
Phasen 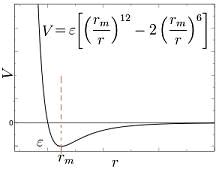 Kraft zwischen zwei Teilchen als Funktion des Abstands: Das Lennard-Jones-(12,6)-Potential mit anziehenden Kräften in 6., abstoßender in 12. Potenz. Minimumpotential bei Teilchenabstand rm grenzen zwischen nichtmischbaren Flüssigkeiten, festen und flüssigen Stoffen oder verschiedenen Körpern, die beiden zugehören, sind Grenzflächen. Wird von Oberflächenspannung bzw. -energie gesprochen, ist die Tension an der Phasengrenze zur Luft (Inertgas, mit dem Dampf der Flüssigkeit gesättigter Luft) gemeint. Zur Unterscheidung bezeichnet Grenzflächenspannung die entsprechende Kraft zwischen kondensierten Phasen. Die Stärke der Grenzflächenspannung ist erkennbar, wenn man beispielsweise zwei nichtmischbare Flüssigkeiten vermengt. Die Phasen trennen sich umso schneller, je größer die Grenzflächenspannung ist – man erhält ein margarineartiges Etwas (Emulsion) bei sehr geringen Grenzflächenspannungen oder eine homogene Lösung. Ober- und Grenzflächenspannung beruhen auf gegenseitiger Anziehung der Teilchen. Gäbe es diese anziehenden (attraktiven) Kräfte nicht, gäbe es keine Phasen, alles wäre Gas. Andererseits gibt es auch abstoßende (repulsive) Kräfte, denn Materie fällt ja nicht in sich zusammen. Die sowohl attraktiv wie repulsiv wirkenden Kräfte (F) sind in den molekularen Dimensionen jedoch von ganz anderer Natur als Schwerkraft oder elektrostatische Kraft. Schwerkraft, elektrostatische und magnetische Kräfte nehmen mit dem Quadrat des Abstand ab (F~1/r2). Wenn molekulare Kräfte ebenso weit reichende Wirkungen hätten wie die Gravitation, die Sonnensysteme zusammenhält, dann würde ganz analog die Oberflächenspannung von der Flüssigkeitsmenge abhängen (bei Nanoteilchen!). - Tatsächlich nehmen molekular anziehende Kräfte in höherer Potenz (F~1/r6) bei Annäherung zu und werden durch abstoßende Kräfte, die in 8- bis 16-Facher Potenz wachsen, vor weiterer Annäherung abgehalten (Mie-, Lennard-Jones- Potential; Abb. links)[72]. Atomar/Molekular attraktive wie repulsive Kraftwirkungen fallen mit dem Abstand in hoher Potenz dramatisch ab und haben folglich nur sehr geringe Reichweiten.
Kraft zwischen zwei Teilchen als Funktion des Abstands: Das Lennard-Jones-(12,6)-Potential mit anziehenden Kräften in 6., abstoßender in 12. Potenz. Minimumpotential bei Teilchenabstand rm grenzen zwischen nichtmischbaren Flüssigkeiten, festen und flüssigen Stoffen oder verschiedenen Körpern, die beiden zugehören, sind Grenzflächen. Wird von Oberflächenspannung bzw. -energie gesprochen, ist die Tension an der Phasengrenze zur Luft (Inertgas, mit dem Dampf der Flüssigkeit gesättigter Luft) gemeint. Zur Unterscheidung bezeichnet Grenzflächenspannung die entsprechende Kraft zwischen kondensierten Phasen. Die Stärke der Grenzflächenspannung ist erkennbar, wenn man beispielsweise zwei nichtmischbare Flüssigkeiten vermengt. Die Phasen trennen sich umso schneller, je größer die Grenzflächenspannung ist – man erhält ein margarineartiges Etwas (Emulsion) bei sehr geringen Grenzflächenspannungen oder eine homogene Lösung. Ober- und Grenzflächenspannung beruhen auf gegenseitiger Anziehung der Teilchen. Gäbe es diese anziehenden (attraktiven) Kräfte nicht, gäbe es keine Phasen, alles wäre Gas. Andererseits gibt es auch abstoßende (repulsive) Kräfte, denn Materie fällt ja nicht in sich zusammen. Die sowohl attraktiv wie repulsiv wirkenden Kräfte (F) sind in den molekularen Dimensionen jedoch von ganz anderer Natur als Schwerkraft oder elektrostatische Kraft. Schwerkraft, elektrostatische und magnetische Kräfte nehmen mit dem Quadrat des Abstand ab (F~1/r2). Wenn molekulare Kräfte ebenso weit reichende Wirkungen hätten wie die Gravitation, die Sonnensysteme zusammenhält, dann würde ganz analog die Oberflächenspannung von der Flüssigkeitsmenge abhängen (bei Nanoteilchen!). - Tatsächlich nehmen molekular anziehende Kräfte in höherer Potenz (F~1/r6) bei Annäherung zu und werden durch abstoßende Kräfte, die in 8- bis 16-Facher Potenz wachsen, vor weiterer Annäherung abgehalten (Mie-, Lennard-Jones- Potential; Abb. links)[72]. Atomar/Molekular attraktive wie repulsive Kraftwirkungen fallen mit dem Abstand in hoher Potenz dramatisch ab und haben folglich nur sehr geringe Reichweiten.
Die Stärke der Grenzflächenspannung beim Kontakt zweier nicht mischbarer Flüssigkeiten, z.B. Öl auf Wasser, mag sich auf den ersten Blick vielleicht einfach aus der Differenz der Oberflächenspannungen von Öl und Wasser ergeben. Das zumindest ist eine Abschätzung aus der Erfahrung. Wenn z.B. die Grenzfläche von Hexan (γ=18 mN/m) und Wasser (γ=73 mN/m) als sich berührende Oberfläche von Hexan und Oberfläche von Wasser angesehen wird, dann würde physikalisch gesehen für eine Doppeloberfläche die Grenzflächenspannung als Summe beider Oberflächenspannungen auftreten (91 mN/m). Dergleichen ist aber nicht der Fall - dergleichen würde schon augenscheinlich aufgefallen sein.
Unter den unpolaren Wechselwirkungen versteht man im engeren Sinne die sog. London-Kräfte (Fritz London 1930). Sie sind in jedem Material vorhanden und kommen zustande, indem Fluktuationen der Elektronendichten ein Dipolmoment erzeugen, das sich über Atome/Moleküle hinweg durch Induktion synchronisiert und damit wechselseitig anziehend wirkt. London-Kräfte beruhen auf der Polarisierbarkeit (Weichheit & Ausmaß) der Elektronenwolke. Sie wirken immer anziehend und können sich additiv verstärken. Ein permanenter Dipol (Teilchen mit asymmetrischer Ladungsverteilung) polarisiert entsprechend die Nachbarschaft und entfaltet dadurch Wechselwirkung. Diese Dipol-induzierte-Dipol-Kräfte heißen Debey-Wechselwirkungen (P. Debey 1921).
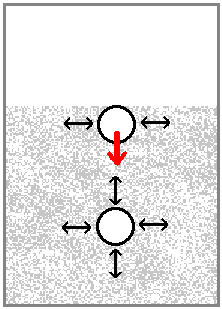
Abb.1: Oberfläche? Eine Flüssigkeitsoberfläche endet sehr abrupt, die Dichte ändert sich um den Faktor ~1000 über die Strecke von einer Molekülschicht und pro cm² Oberfläche und Sekunde wechseln 1021 Moleküle die Phase (Wasser bei 20°C)[62, S.72]. Die Flüssigkeitsoberfläche ist ein turbulenter Ort; zunehmend bei geringerer Oberflächenspannung. Bei der kritischen Temperatur verschwindet die Oberflächenspannung und die Oberfläche.
Die Oberflächenspannung ist die Summe aus allen in der Phase wirkenden attraktiven wie repulsiven Kräfte. Anhand von Messungen der Grenzflächenspannung kann unter Variation der Grenzflächenpartner auf Vorhandensein, Ausmaß und die Zuordnungen der Kräfte geschlossen werden.
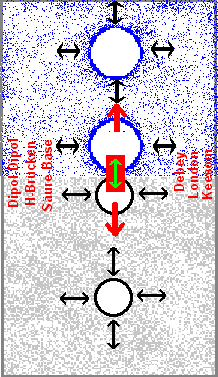
Abb.2: Die Grenzflächenspannung zwischen zwei Flüssigkeiten ist immer kleiner als die Differenz der Grenzflächenspannungen beider Flüssigkeiten gegen die Luft, weil stets irgendwelche kompatiblen Potentiale über die Phasengrenze wechselwirken.
1.2 Physiologische Aspekte
Angaben zur Oberflächenenergie von Biopolymeren, Enzymen, Zucker/Stärke, Bakterienoberflächen[71] bewegen sich im Bereich γs ~ 43 ±5 mN/m. Interessant hierzu ist, sich die Betrachtung der (Gefährdungs-)Klassifikation verschiedener Lösemittel oder Präparationen vor Augen zu führen. DMSO (Dimethylsulfoxid, 44 mN/m) dringt leicht in die Haut und andere Zellmembranen ein und kann Wirkstoffe als Transportvermittler einschleusen; Chlorbenzol (34 mN/m) führt zu starken Hautreitzungen. Benzaldehyd (38 mN/m) und Nitrobenzol (44 mN/m) können durch die Haut aufgenommen werden. Eine Penetrationsförderung in die Haut wird PEG nachgesagt (Polyethylenglycol 200 mit 43,5 mN/m) - jedoch Diethylenglycol (44 mN/m) wird angeblich nur geringfügig durch die Haut resorbiert. Es ist unklar, inwiefern polar-, unpolar- oder Säure/Base- Komponenten der Oberflächenenergie eine Rolle spielen. Zu Oberflächenenergie-Komponenten finden Sie weiter unten auf dieser Seite noch eine Abhandlung. - Weiterhin ist im Umlauf, dass Waschmittelformulierungen bzw. Tenside mit niedrigerer CMC und Oberflächenspannung weit bessere Hautverträglichkeit zeigen und weniger reizen als Detergenzien mit geringerer Effizienz (d.h. höherer CMC).
Flüssigkeiten höherer Oberflächenspannungen (Glycerin, Formamid, Wasser) werden offenbar nicht durch die Haut aufgenommen. Gleichwohl können ähnliche Wirkungen wie bei Flüssigkeiten mit geringer Oberflächenspannung auftreten. So sind beispielsweise die Oberflächenspannungen von Isopropanol, Oktan und Ethanol vergleichbar niedrig, sie betragen 21-22 mN/m. Wenn man mit einem Schwämmchen die Finger betupft, merkt man, dass besonders Oktan die Haut entfettet, weniger bei Isopropanol und noch weniger bei Ethanol. Hier ist wohl schlicht die Löslichkeit von Fingerfett im Lösemittel zu bemerken, eine Permeation tritt nicht auf.
1.3 Beispiele zur Messung der Grenzflächenspannung
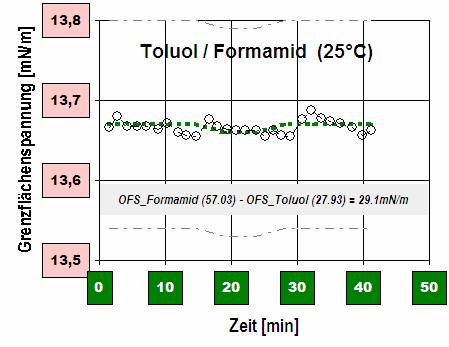
Diagramm 1: Toluol und Formamid sind wie Wasser und Öl nicht mischbar. - Die Grenzflächen-spannung zwischen Toluol und Formamid, über 40 Minuten hinweg per Ringmethode gemessen.
(Besonders in Bereichen mit zweifelhaften Referenzdaten ist es sinnvoll, auch eine statisch angenommene Messgröße über eine gewisse Zeit zu verfolgen – zum Einen, um einen guten Mittelwert zu erhalten, zum Anderen, um sicherzustellen, dass im vermeintlichen Endzustand ein Gleichgewicht vorliegt.)
Die Grenzflächenspannung ist bei 13.7mN/m stabil. - Die Differenz der beiden Oberflächenspannungen bei 25°C von Formamid (57.03 mN/m) und Toluol (27.93mN/m) wäre also mit 29.1mN/m weit größer als der tatsächliche Messwert.
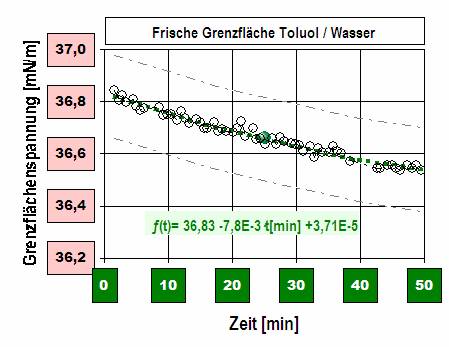
Diagramm 2: Eine frisch erzeugte Grenzfläche zwischen Toluol und Wasser. Sie verändert ihren Wert. Für die Grenzflächenspannung zwischen Toluol und Wasser wird ein Wert von 31 mN/m gemessen, wenn die beiden Flüssigkeiten intensiv vermischt werden. Ein kleiner Anteil Wasser löst sich im Toluol und etwas Toluol auch im Wasser. In der Literatur werden in der Regel Grenzflächenspannung zwischen gegenseitig gesättigten Flüssigkeiten angegeben.
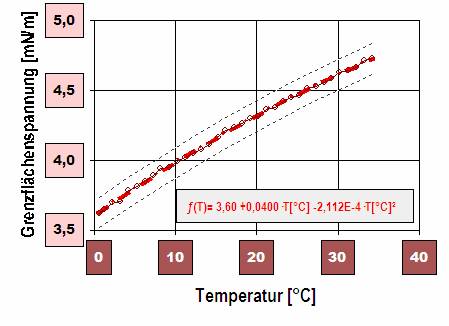
Diagramm 3: Temperaturabhängigkeit der Grenzflächenspannung zwischen tensidhaltigem Wasser und Toluol.
(Wasser mit 5 g/L SDS [Sodium Laureth Sulfate, Laurylsulfat], CMC von SDS =2.3g/L)
Die Oberflächenspannung reiner Stoffe nimmt praktisch ausnahmslos mit der Temperatur ab. Bei der Grenzflächenspannung nennt die Literatur[15, S.25, Fig.9] Ausnahmen, Heptin, Heptylaldehy und höhere Paraffine gegenüber Wasser.
Der positive Gradient dγ / dT, Zunahme der Grenzflächenspannung bei steigender Temperatur, bedeutet Entropieabnahme (Überschussentropie S(A)) in der spezifischen Grenzfläche. "Die Ordnung der Grenzfläche nimmt gegen die in der Bulkphase zu."
Die Diagramme entstammen IMETER-Prüfberichten; Diese finden sich unter --> Oberflächenspannung, Beispiele und können als PDF heruntergeladen werden.
1.4 Benetzung, Kontaktwinkel, Kontaktwinkelhysterese
Während die O 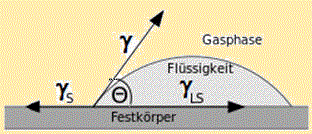 berflächenspannung von Flüssigkeiten der direkten Messung zugänglich ist, nämlich durch die Bestimmung der Kraft, die der Erzeugung neuer Oberfläche entgegensteht, ist die Oberflächenspannung fester Körper praktisch nur indirekt messbar. Die Oberflächenspannung charakterisiert die einzelne Flüssigkeit. Sie bestimmt beispielsweise die freie Tropfenform und -größe oder auch den Druck in Gasblasen (Hohlräumen). Zwischen nichtmischbaren flüssigen Phasen ist die Stabilität beider Phasen jeweilig von der adhäsiv wirkenden Grenzflächenspannung und der kohäsiven Oberflächenspannungen der Einzelflüssigkeiten abhängig. Bei Benetzung und Benetzbarkeit der Wechselwirkung flüssiger und fester Stoffe sind die Verhältnisse der Ober- und Grenzflächenspannungen der hier nun beteiligten drei Phasen in Betracht zu ziehen. Bei Feststoffen erzeugt der Begriff 'Oberflächenspannung' Verwirrung, weil diese mechanische Spannung nicht so unmittelbar erkennbar ist - bei fester Materie ist es darum üblich, den allgemeinen Begriff Oberflächenenergie zu verwenden.
berflächenspannung von Flüssigkeiten der direkten Messung zugänglich ist, nämlich durch die Bestimmung der Kraft, die der Erzeugung neuer Oberfläche entgegensteht, ist die Oberflächenspannung fester Körper praktisch nur indirekt messbar. Die Oberflächenspannung charakterisiert die einzelne Flüssigkeit. Sie bestimmt beispielsweise die freie Tropfenform und -größe oder auch den Druck in Gasblasen (Hohlräumen). Zwischen nichtmischbaren flüssigen Phasen ist die Stabilität beider Phasen jeweilig von der adhäsiv wirkenden Grenzflächenspannung und der kohäsiven Oberflächenspannungen der Einzelflüssigkeiten abhängig. Bei Benetzung und Benetzbarkeit der Wechselwirkung flüssiger und fester Stoffe sind die Verhältnisse der Ober- und Grenzflächenspannungen der hier nun beteiligten drei Phasen in Betracht zu ziehen. Bei Feststoffen erzeugt der Begriff 'Oberflächenspannung' Verwirrung, weil diese mechanische Spannung nicht so unmittelbar erkennbar ist - bei fester Materie ist es darum üblich, den allgemeinen Begriff Oberflächenenergie zu verwenden.
Flüssigkeitstropfen auf glatten Festkörperoberflächen liegen, wenn sie nicht völlig verlaufen (spreiten), mehr oder weniger flach oder steil auf der Oberfläche. An der Grenzlinie, an der die drei Phasen (Vakuum/Gas-flüssig-fest) aufeinander treffen, bilden sich die herrschenden Energieverhältnisse in der Form ab, in der sich die Flüssigkeit auf der festen Oberfläche anschmiegt. Das Charakteristische der Anschmiegung ist der Winkel zwischen Fluid- und Feststoffoberfläche an der Grenzlinie. Dieser Kontaktwinkel wird gemessen, indem über die Tropfenmitte hinweg eine Tangente zur Dreiphasenlinie angelegt wird (vgl. Abb.). Die Verhältnisse der Oberflächenenergien werden durch die sog. Young-Gleichung[19 , 20] beschrieben:
cos Θ = ( γs - γls ) / γ [Gl.1.3.1] (Young-Gleichung)
γs Oberflächenenergie des Festkörpers (= γs,g )
γls Grenzflächenspannung zwischen Flüssigkeit und Festkörper (= γ12 )
γOberflächenspannung der Flüssigkeit gegen ihren eigenen Dampf (= γl,g)
Die Differenz γs - γls kann nur größer oder gleich Null sein und wird Benetzungsspannung genannt. Der Winkel Θ ("Theta") ist der Rand-, Kontakt-, Young- oder Benetzungswinkel. Er kann Werte in den Grenzen 0° ≤ Θ < 180° annehmen. Man sagt, eine Flüssigkeit wirkt benetzend bzw. der Festkörper ist benetzbar, wenn der Kontaktwinkel Θ<90° beträgt. Die Güte der Benetzung ist dem Randwinkel indirekt proportional. Der Randwinkel von z.B. Quecksilber auf Glas beträgt etwa 138°, Glas wird von Quecksilber absolut nicht benetzt.
Im Gegensatz zum Fall Θ = 0°, der totalen Benetzung (Spreitung), kann Θ = 180°, die totale nicht-Benetzung, nicht zu Stande kommen, weil in und zwischen kondensierten Phasen immer Anziehungskräfte auftreten (London-Kräfte). Im Falle von Wasser spricht man bei Kontaktwinkeln Θ>90°von Hydrophobie und ab ca. 120° von Superhydrophobie; Omniphob wären Oberflächen, die sich von keiner Flüssigkeit benetzen lassen.
Phänomen "Lotuseffekt": Er beruht nicht auf den reinen Wirkungen der Oberflächenenergien, sondern besonders auf Struktureffekten. Die Oberflächenenergie z.B. von Wachspartikeln,die Pflanzen ausbilden können, ist so gering auch wieder nicht. Die Grundlage des Effektes ist (zumindest teilweise) in der Wenzelgleichung gegeben: cos Θgem.= r·cos Θ.
Sie bedeutet, dass der Kontaktwinkel realer Oberflächen noch besonders durch die Rauhigkeit r der Oberfläche festgelegt ist. Der gemessene Kontaktwinkel (Θgem.), d.h. der Randwinkel des Wassertropfens auf dem Blatt der Lotuspflanze, ist mit einem 'Verstärkungsfaktor' versehen. Die Rauheit r verstärkt den materiell bedingten Effekt. Idealglatte Oberflächen haben ein r=1, bei realen Oberflächen ist r immer größer als 1. Bei schlechter Benetzung, wo bereits ein materielles cos Θ>90 auftritt, wird der Kontaktwinkel durch die Rauhigkeit (Strukturierung) weiter vergrößert. Die Struktur der oberflächenreich dargebotenen Wachspartikeln in Lotus-Blütenblättern führt zu Kontaktwinkeln bis über 160°. Man kann sich diesen Zusammenhang leicht selbst verdeutlichen, indem man ein Stück Kunststoff mit einer Nagelfeile schleift, vor- und nachher in Wasser taucht und dann das selbe - zu gegenteiligem Effekt - mit einem Glas- oder Platinplättchen tut. (Bei Oberflächen, die aus zwei Materialarten zusammengesetzt sind, gilt die sog. Cassie-Baxter Gleichung [eng.Wiki])
Die Oberflächenenergie des Festkörpers γs ist die vorliegende, die zu Tage tretende, gemessene Oberflächenenergie; sie ist nicht unbedingt die Oberflächenenergie des reinen Materials. Der Festkörper, im Gleichgewicht mit dem Flüssigkeitsdampf, hat (ggf.) Dampf adsorbiert und seine Oberflächenenergie ist verringert:
γs = γs° - πe d.h. γs° = γs + πe [Gl.1.3.2]
πe ist der Gleichgewichtsdruck bzw. der Ausbreitungs- oder Spreitungsdruck des Flüssigkeitsdampfes an der Oberfläche im Gleichgewicht. Im Vakuum ist πe Null und die vorliegende Festkörperoberflächenenergie hat den Vakuumwert (γs° = γs ).
Bei Kontaktwinkelmessungen ist es allgemeine Praxis πe = 0 anzunehmen. Das ist eigentlich nicht korrekt, aber πe ist messtechnisch schwierig zu bestimmen und wird schließlich bei "γ > γs" als unbedeutend eingeordnet [71, S.133].
Unter Adhäsionsarbeit (Wa) wird die reversible Oberflächenarbeit (auch differenzielle Grenzflächenarbeit genannt) verstanden, die zum Ablösen der Benetzung vom Untergrund erforderlich ist (Dupré 1869):
Wa = γs+ γ - γls [Gl.1.3.3]
Über die Freie Enthalpie (G) formuliert als freie Adhäsionsenthalpie (ΔGls), Wa =-ΔGls (T,p,V,n):
ΔGls = - γs - γ + γls [Gl.1.3.4]
(wir verwenden jedoch im Weiteren für "freie Enthalpie" den Englischen Begriff der freien Energie, der Gibbs-Energie)
Der Zusammenhang von Kontaktwinkel und Thermodynamik kann aus der Young-Dupré Gleichung also folgendermaßen geschrieben werden:
-ΔGls = γ(1+cos Θ) [Gl.1.3.5]
Der Größte Wert, der für Wa bzw. -ΔGls erhalten werden kann, wenn also cos Θ= 1 ist (bei totaler Benetzung), bedeutet dass die Arbeit maximal die doppelte Oberflächenspannung der Flüssigkeit erreicht (= Kohäsionsenergie). Es müssen ja zwei Oberflächen, da abgetrennt, neu erarbeitet werden.
Kontaktwinkelhysterese
Warum bleibt z.B. in einem Trinkhalm bisweilen etwas der Flüssigkeit festgehalten? Folgende Skizze und Formel zeigen, wie die beiden Benetzungswinkel eine bestimmte Menge Flüssigkeit in einer Röhre festhalten können [Lit. 84, S.70]. - Sobald die Höhe der Flüssigkeitsschicht L übersteigt, also ein Mindestgewicht erreicht, folgt sie der Schwerkraft und fließt ab:
 [Gl.1.3.6]
[Gl.1.3.6]
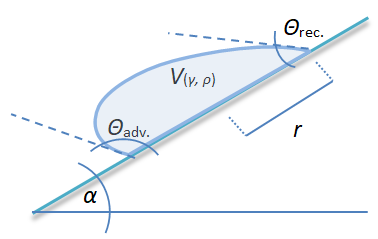 Der Fall von Fluidbrücken in einer Kapillare ist physikalisch gut beschreibbar. Mathematisch und messtechnisch erheblich schwieriger ist die Modellierung für liegende Tropfen (Bild rechts), wobei deren Praxisbezug vielfach gegeben ist. Quéré [Lit. 102] gibt eine Gleichung an, die jedoch nur für relativ kleine Kontaktwinkelhysteresewerte und kreisrunde Kontaktflächen anwendbar ist:
Der Fall von Fluidbrücken in einer Kapillare ist physikalisch gut beschreibbar. Mathematisch und messtechnisch erheblich schwieriger ist die Modellierung für liegende Tropfen (Bild rechts), wobei deren Praxisbezug vielfach gegeben ist. Quéré [Lit. 102] gibt eine Gleichung an, die jedoch nur für relativ kleine Kontaktwinkelhysteresewerte und kreisrunde Kontaktflächen anwendbar ist: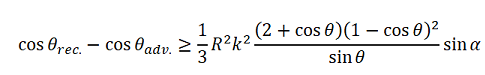 [Gl.1.3.7]
[Gl.1.3.7]mit R=r/sinΘ; Θ=(Θadv+Θrec)/2 und Kapillarkonstante k = √(γ/ρg)
Die Gleichung erlaubt die Schätzung, ab welchem Neigungswinkel α ein Tropfen in Bewegung gerät.
Während in der zitierten Literatur für Θ der Mittelwert, (Θadv+Θrec)/2, eingesetzt wird, wird oft aus den Θadv und Θrec - Werten der Kontaktwinkel Θ nach der Formel von Tadmor berechnet (vgl. Artikel in en-Wikipedia).
 pritzten Oberfläche sehr uneinheitliche Tropfenformen erkennen können (vgl. Bild rechts) . Der Kontaktwinkel kann zwischen den Werten von Θadv bis Θrec alle möglichen Werte annehmen. Entsprechend können auch größere Einzeltropfen ein Spektrum verschiedener Kontaktwinkel aufweisen. Das Ausmaß der Kontaktwinkelhysterese kann ein Qualitätsmerkmal sein, etwa für die Ablaufneigung von Regen auf der Windschutzscheibe, in der Flotationstechnik (Trennverfahren) und generell bei Vorgängen, wo Phasengrenzen vermengt werden (z.B. das Festhalten von [Gas-]Bläschen in Geweben).
pritzten Oberfläche sehr uneinheitliche Tropfenformen erkennen können (vgl. Bild rechts) . Der Kontaktwinkel kann zwischen den Werten von Θadv bis Θrec alle möglichen Werte annehmen. Entsprechend können auch größere Einzeltropfen ein Spektrum verschiedener Kontaktwinkel aufweisen. Das Ausmaß der Kontaktwinkelhysterese kann ein Qualitätsmerkmal sein, etwa für die Ablaufneigung von Regen auf der Windschutzscheibe, in der Flotationstechnik (Trennverfahren) und generell bei Vorgängen, wo Phasengrenzen vermengt werden (z.B. das Festhalten von [Gas-]Bläschen in Geweben). An liegenden Tropfen können goniometrische Kontaktwinkelmessungen unter variantenreichen Bedingungen stattfinden: Der Tropfen kann mittels Kanülen aufgebläht und abgesaugt werden, um entsprechende Vorrück-/Rückzugswinkel zu bestimmen, man kann Tropfen trocken lassen, um Rückzugswinkel zu bestimmen, auf Neigetischen vermessen (Twistet Plate, wie im Bild oben), auf rotierenden Tischen, um per Zentrifugalkraft die Kontaktwinkel zu variiern, oder dynamische Kontaktwinkel an den bewegten Phasengrenzen ermitteln, oder vibrierende Tische verwenden, um so den Kontaktwinkelwert ggf. hysteresefrei zu messen. Wie stehen die Winkel im Zusammenhang mit dem Kontaktwinkel in der Young-Gleichung (Gl.1.3.1)? Ausserdem ist der Kontaktwinkel in allen thermodynamischen Zusammenhängen eine statische Größe. Auch die Frage nach der Tropfengröße kann durch Kontaktwinkelmessungen mit der Wilhelmy Methode Typ II (IMETER Methode N°4) elegant umgangen werden.
Die beiden Diagramme, unten, zeigen die Benetzungs- und Auftriebskraft bei einem gereinigten Objektträgergläschen beim Ein- und Austauchen in Wasser (Eintauchwerte rot, Austauchwerte grün). Beim linken Diagramm wurde die Glasplatte nach der Reinigung für die Dauer von zwei Tagen in einem Eksikkator aufbewahrt, im rechten unmittelbar nach der Reinigung getrocknet und gemessen:
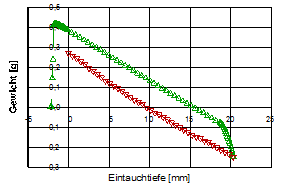
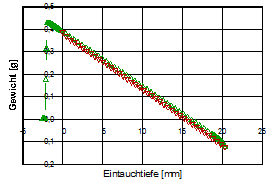
(ID12468, 9)
Um Auftriebskräfte korrigiert und bezogen auf den Umfang des Glasplättchens erhält man aus den Daten des linken Plots das Digramm unten. Die entsprechenden Θadv (▲) und Θrec (▼)- Werte werden angezeigt - rechts der Bereich der Hysterese.
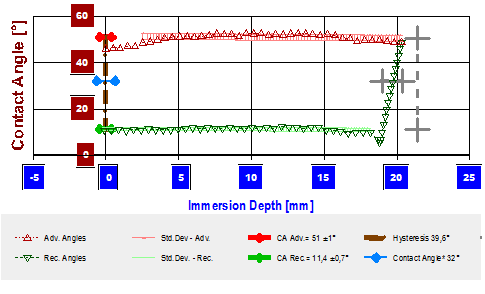
1.5 Ermittlung der Festkörperoberflächenenergie
Bei bekannter Oberfläche kann kalorimetrisch aus der Benetzungswärme die Oberflächenenergie abgeleitet werden. Bei schmelzbaren Stoffen kann aus Messungen der Oberflächenspannung der Flüssigkeit bei verschiedenen Temperaturen die Oberflächenenergie des Feststoffs extrapoliert werden (mit typisch 10-20% Unterschätzung [Lit. 83, S.287]). Eine direkte Messung bei der Schaffung neuer Festkörperoberfläche ist praktisch nicht durchführbar (Zugversuch [Lit. 15, S.3]), d.h. quantenmechanische Berechnungen (Dichtefunktionaltheorie) und direkte Kraftmessungen (gekreuzte Zylinder [Lit. 78, S.240]) stehen eher nur theoretisch zur Verfügung. Der praktikable Zugang zur Oberflächenenergie von Feststoffen erfolgt durch indirekte Messung, nämlich durch die Interpretation von Kontaktwinkeln. Diese bietet sich besonders dann an, wenn die in Natürlichkeit mit Adsorbat vorliegende, reale Materialoberfläche von höherer Relevanz als der theoretische Aspekt der idealreinen Feststoffoberfläche ist. Die Messung von Kontaktwinkeln kann optisch (Goniometer) oder durch Wägeverfahren (Washburn-Methode, PUK, Wilhelmyplatte Typ II) erfolgen. Dünnschicht- (TLC) und inverse Gas- Chromatographie seien noch erwähnt. -- Zur Auswertung der Kontaktwinkeldaten gibt es verschiedene Verfahren:
- Die kritische Oberflächenspannung der Benetzung γkrit.=> Methode von Fox und Zismann (1950)
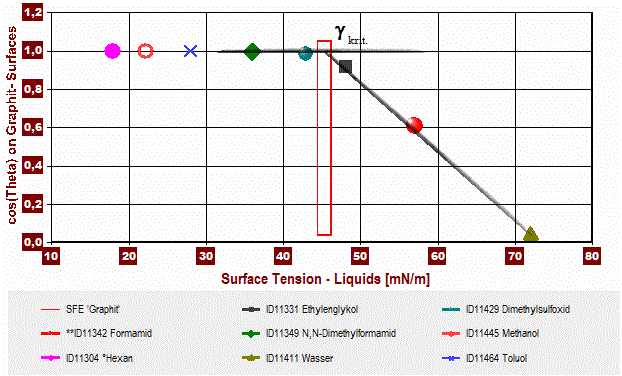
[Diagramm 4] (Grafit-Pulver) In der Zisman-Darstellung werden in einem Diagramm die gemessenen cosΘ-Werte gegen die Oberflächenspannung des Fluids angetragen. Sofern sich eine fallende, lineare Proportionalität einstellt, kann die Gerade auf cosΘ ⇒ 1 (d.h. Θ = 0°) verlängert einen oberen Grenzwert für die Oberflächenspannung der Flüssigkeit liefern, die den Festkörper gerade vollständig benetzt (γkrit..: 'die kritische Oberflächenspannung der Benetzung' [critical surface tension of wetting]). Die Methode hat Ähnlichkeiten zum einfachen Testtinten-Verfahren.
Der Wert von γkrit. befindet sich stets in der Nähe von γs. Je nachdem welche homologe Reihe von Testflüssigkeiten angewendet wird (n-Alkane, Alkylbenzole, Ether, Siloxane, ...), werden jedoch deutlich unterschiedliche γkrit.-Werte ermittelt [67, S.367]. So wurde vorgeschlagen, anstelle von γ nur die unpolare Komponente der Oberflächenspannung (γLW bzw γd) an der X-Achse anzutragen [93] und für Θ den Wert von Θadv einzusetzen.
- Nach Neumann's "Equation of State" (1967) ist die Festkörperoberflächenenergie γs über einen Kontaktwinkel Θ einer Flüssigkeit (Oberflächenspannung γ) unmittelbar verbunden:
![neumann eq state]()
- γ (1+cos Θ) = 2(γ· γs)1/2 · e – β ( γ - γs)² [Gl.1.4.1]
(Universelle Konstante β = 0,1247 m²/J)
Zur Vorhersage von Kontaktwinkeln auf unpolaren Oberflächen liefert die Gleichung Ergebnisse, die mit Beobachtungen oft übereinstimmen. Bei der Equation of State tritt in anderen Fällen das Problem auf, dass "Flüssigkeiten mit gleichen Oberflächenspannungen verschiedene Kontaktwinkel zeigen". Die nachfolgend umrissenen Verfahren lösen dieses Grundproblem, indem die Oberflächenenergie als Summe aus verschiedenen Wechselwirkungen zusammengesetzt verstanden wird, so wie in der Einführung angesprochen.
-
Fowkes (1962) schlägt vor, die Oberflächenenergie als summativ aus verschiedenen molekularen Wechselwirkungsenergien zusammengesetzt aufzufassen. Das sind Wechselwirkungen von dispersiver (d), polarer (p) und metallischer (m) Natur sowie Kräfte, die auf Wasserstoffbrücken- (h) und Säure-Base-Wechselwirkungen (sb) beruhen:
γ = γd+ γp+ γh+ γsb+ γm [Gl.1.4.4]
Wechselwirkungen finden ausschließlich über gleichartige Komponenten statt. Bei Betrachtung rein dispersiver Wechselwirkungen, wie sie in Alkanen (aliphatischen Kohlenwasserstoffen) vorliegen und bei Polymeren entsprechend in PE, PP, PTFE anzutreffen sind, fallen die anderen Komponentenglieder weg und es gilt:
γ (1+cos Θ) = 2(γd·γsd)1/2 [Gl.1.4.5]
-
Die so genannte erweiterte Fowkes- Gleichung (extended Fowkes) [94] verwendet drei Glieder:
γ (1+cos Θ) = 2(γd'· γsd')1/2 + 2(γp'· γsp')1/2 + 2(γh · γsh)1/2 [Gl.1.4.5A]
Die Methode ermöglicht polare Materialien zusätzlich über ihren Anteil an Wasserstoffbrückenbindungen γsh zu charakterisieren.(Komponentendaten der Flüssigkeiten vgl. Tabelle unten). Die Berechung erfolgt klassisch in Stufen; (heute) einfacher ist die Lösung eines überbestimmten, linearen Gleichungssystems. Weitergehende Ausführungen von Gl.1.4.4 sind praktisch unbekannt.
-
Owens, Wendt, Rabel und Kaelble (1969,70) -- "OWRK" -- wenden die Fowkes-Theorie mit γd- und γp-Komponenten auf Kontaktwinkeldaten an:
γ (1+cos Θ) = 2((γd· γsd)1/2 + (γp· γsp)1/2) [Gl.1.4.6]
Zwei Kontaktwinkelmessungen genügen im Prinzip, um die Unbekannten γsd und γsp zu bestimmen (γs= γsd+γsp). Bei mehreren Kontaktwinkeldaten gibt es für OWRK ein grafisches Lösungsverfahren, worin die Spezialität dieser Methode besteht. Aus Gl.1.4.6 ergibt sich mit
![OWRK Gl]() eine Geradengleichung, deren Steigung √ γsp entspricht; der Achsenabschnitt beträgt √ γsd .
eine Geradengleichung, deren Steigung √ γsp entspricht; der Achsenabschnitt beträgt √ γsd .
Um die grafische Auswertung durchzuführen, werden die Koordinaten einer Kontaktwinkelmessung gemäß
![OWRK xy]() in ein Diagramm eingetragen:
in ein Diagramm eingetragen:
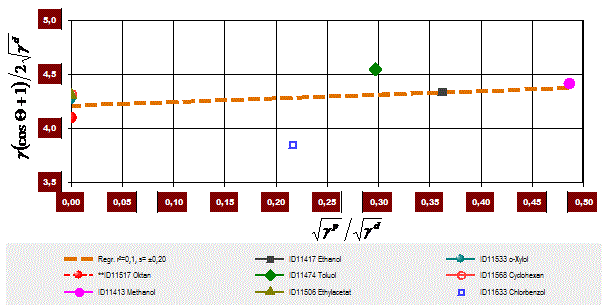
Daneben führt das Diagramm die Qualität der Korrelation vor Augen.
Die nachfolgende Abbildung zeigt, wie sich erhaltene γsd und γsp -Messergebnisse anschaulich darstellen lassen.
![Benetzungsdiagramm, Wetting-Zones (Wetting-Envelop) für ein spezielles Glas [IMETER 11637] Wetting Alkaliglas](https://imeter.de/images/ART/M7/Wetting_Alkaliglas.gif)
[Diagramm 6] Vorhersagen über Kontaktwinkel und Benetzbarkeiten aus den dispers-polar-Verhältnissen: 'Wetting-zones' zu pulverisiertem Alkaliglas - In dem Koordinatensystem werden an der X-Achse jeweils dispersive und auf der Y-Achse polare Komponentenwerte eingezeichnet. Ein dunkelrot gezeichnetes Kreuz mit Umkreis (inmitten blauer Ringe) gibt die Koordinaten des "Ergebnisses" an. Der Mittelpunkt liegt auf der roten Linie - sie gibt diejenigen dispers-polar-Werte an, mit denen Flüssigkeiten einen Kontaktwinkel von Null erreichen würden; dispers-polar-Kombinationen, die auf der Linie und innerhalb der Umrahmung liegen, führen demnach zu totaler Benetzung. Außerhalb (darüber und rechts) treten Kontaktwinkel auf. (Diese Darstellung wird auch 'Wetting Envelope' genannt.) Die grüne Linie gibt in gleicher Weise den Vorhersagebereich für Kontaktwinkel von 45° an. Die in der Untersuchung verwendeten Flüssigkeiten sind als Kugeln eingetragen. Die Ergebniskoordinaten sind 'umkreist' von drei blauen Ringen - diese verorten Bereiche der Grenzflächenspannung von 0.1, 0.5 und 1 mJ/m². Die Grundlage der Kalkulationen im Wetting-zones Diagramm ist (γd+γp)·(cosΘ + 1) = 2·√(γsd·γd) + 2·√(γsp·γp).
-
G. X. Wu (1982) schlägt die Berechung über das harmonisches Mittel vor:
γ (1+cos Θ) = 4 ((γd· γsd) / (γd+ γsd) + (γp· γsp) / (γp+ γsp)) [Gl.1.4.7]
Festkörperoberflächenspannungen lassen sich nach der Wu-Gleichung durch Kontaktwinkelmessungen mit zwei Flüssigkeiten beschreiben. Die Gleichung kann jedoch nicht - so wie die anderen - als lineares Gleichungssystem gelöst werden. Hier können Kontaktwinkel mit reindispersen Flüssigkeiten verwendet werden, um zuerst γsd ausrechnen (der Termteil mit γsp fällt dabei weg), dann γsd einsetzen und im zweiten Schritt durch Einsetzen auch γsp und schließlich γs ermitteln zu können. (Wie bei Fowkes haben sich auch hier noch andere Rechenverfahren etabliert, die zu leicht divergierenden Ergebnissen führen können.)
-
Van Oss, Good und Chaudhury (1987), "OGC", fassen die Komponentenenergien der drei elektrodynamischen Wechselwirkungen (London, Debey und Keesom) zum apolaren Lifshitz - Van der Waals - Anteil (LW) zusammen. Die polaren Wechselwirkungen werden dem Elektronen Akzeptor-Donor-Modell der Lewissäure/Base - Wechselwirkungen zugeordnet:
γ (1+cos Θ) = 2(γLW· γsLW)1/2 + 2(γ+· γs-)1/2 + 2(γ - · γs+)1/2 [Gl.1.4.8] wobei
γs = γs LW + γs AB mit γs AB = 2(γs +· γs -)1/2 und
γ = γLW + γAB mit γAB = 2(γ+· γ-)1/2
Kontaktwinkel mit mindestens drei entsprechenden Messflüssigkeiten sind für diese Berechung erforderlich. Anders als bei Extended Fowkes, wo ja ebenfalls drei Komponenten auftreten, ist die Komponenten-Wechselwirkung der AB (Säure-Base) Komponenten gegensinnig. Materialien können ohne AB-Anteil sein (unpolar), nur eine Säure- oder Base- Wechselwirkung aufweisen (Monopolar) oder über beide Anteile verfügen (bipolar). So können Grenzflächenenergieen auf sieben (bzw. zehn) unterschiedlichen γ+,γ- -Kombinationen beruhen.
Zur Fixierung der Lewis-Säure-Base -Parameter dient Wasser, dem für 20°C die Werte γ =72.8, γ LW=21.8, γ AB=51, γ + =25.5, γ - = 25.5 mJ/m² zugewiesen sind. Bei γ AB kommt zwar nur dem Verhältnis von γ + und γ - relativ zum Bezug eine Bedeutung zu; "2·√( γ +· γ-)" muss jedoch 51 mJ/m² ergeben. Denn γ LW = 21.8 mJ/m² ist Primat aus reindispersen Wechselwirkungen von Wasser (zu den rein-unpolaren Alkanen) und 51 mJ/m² sind γ AB zuzuordnen. - Aufgrund der Festlegung erscheinen Feststoffoberflächen nach OGC fast immer Lewis-basisch. Damit eine der Empirie nicht widersprechende AB-Charakterisierung ermöglicht wird, gibt es alternative Vorschläge für das AB-Bezugssystem [96, 97].
Tabelle 1: Oberflächenspannungen und Komponentenzuordnung einiger gebräuchlicher Messflüssigkeiten in mJ/m²:
| Fowkes, OWRK | ext. Fowkes | OGC | |||||||
| (20°C), mJ/m² |
γ |
γd | γp | γd' | γp' | γh | γLW | γ+ | γ - |
| Wasser | 72,80 | 21,8 | 51 | 29,1 | 1,3 | 42,4 | 21,8 | 25,5 | 25,5 |
| Glycerin | 64 | 34 | 30 | 37,4 | 0,2 | 25,8 | 34 | 3,92 | 57,4 |
| Formamid | 58,2 ª | 39 | 19 | 35,1 | 1,6 | 21,5 | 39 | 2,28 | 39,6 |
| Ethylenglycol | 47,7 ª | 30,9 | 16,8 | 30,1 | 0 | 17,6 | 29 | 3 | 30,1 |
| 1-Oktanol | 27,5 | 27,5 | 0 | n.a. | n.a. | n.a. | 27,5 | 0 | 3,97 |
| Oktan | 21,62 | 21,62 | 0 | 21,62 | 0 | 0 | 21,62 | 0 | 0 |
| Chloroform | 27,15 | 27,15 | 0 | n.a. | n.a. | n.a. | 27,15 | 1,5 | 0 |
Datenquellen [71, S.213f], [83, S.337], []. ª Hier sind geringfügige Unstimmigkeiten in der Relation "γ = γd + γp = γd' + γp' + γh = γLW + 2(γ+ γ - )1/2 ".
Bemerkungen: Auf der Seite http://www.accudynetest.com/polytable_01.html sind Oberflächenenergien, Kontaktwinkel und Komponentendaten zu Polymeren zu finden. Die Streubreiten der Angaben sind im Allgemeinen leider ziemlich groß. Dass dem so ist, wird erkennbar, wenn man bei den vorgenannten Mess- und Rechenverfahren mehr als die Mindestanzahl von zwei oder drei Flüssigkeiten für Messungen verwendet und sich entsprechende Standardabweichungen ergeben. Aus Tradition und weil einzelne Verfahren sich Stofftypisch bewährt haben, werden alle genannten Verfahren / Theorien heute verwendet, obwohl Neumann's Equation of State und Wu's harmonisches Mittel längst als inkorrekt beurteilt werden [62, S.292f; 71, S.166ff]. Bei anderen Geräteherstellern findet man Anwendungsregeln für die Rechenmethoden wie, "Wu wird mehr für niederenergetische Wechselwirkungen der Oberflächen, das geometrische Mittel (OWRK) mehr für Wechselwirkungen zwischen nieder- und hochenergetischen Stoffen verwendet". Die Regeln sind teilweise widersprüchlich. Die IMETER-Auswertung macht es sich in gewisser Weise einfach und berechnet nach allen Modellen, für die Experimental- und Fluiddaten vorhanden sind.
Die Angaben von ermittelten Festkörperoberflächenspannungen sollten immer unter Nennung der Berechnungsmethode erfolgen; die verwendeten Kontaktwinkel- und Komponentendaten sollten ebenfalls angegeben werden.
1.6 Bedeutung der Ober- und Grenzflächenenergie nach OGC [71]
Die Theorie von van Oss, Good und Chaudhury (OGC) gilt als modernster und leistungsfähigster Ansatz. Sie ermöglicht aus der Oberflächenenergie (d.h. aus Kontaktwinkeldaten) Vorhersagen hinsichtlich der Mischbarkeit/Verträglichkeit von Stoffen und erlaubt Adhäsionseffekte zu quantifizieren. Im Unterschied zu Fowkes/OWRK kann OGC abstoßend wirkende Kräfte beschreiben.
Nachfolgend sind die Regeln zur Berechnung der Interaktionspotentiale in Ein-, Zwei- und Drei- Phasensystemen angegeben:
-
Kohäsionsenergie im Material 1 (ΔG11 ):
Oberflächenspannung, Energiegewinn durch Verkleinerung der Oberfläche.
ΔG11= -2γ1 = - (γ1LW + γ1AB) = - (γ1LW + 2√(γ1+ γ1-)) [Gl.1.5.1]
-
Adhäsionsenergie zwischen Material 1 und Fluid 3 oder Material 2 (ΔGA ,ΔGls , ΔG12 , ΔG13 ):
Grenzflächenspannung, Energiegewinn durch Zusammenlagerung und Bildung einer gemeinsamen Grenzfläche.
ΔGls= -2γ1s = -2√(γLW γsLW) - 2√(γ+ γs-) - 2√(γ - γs+) [Gl.1.5.2]
γls = γs + γ - 2√(γLW γs LW) + 2√(γ+γs -) + 2√(γ - γs +)
-
Adhäsionsenergie zwischen Materialien 1 vermittels Fluid 3(ΔG131 , [ΔG121 ]):
Grenzflächenenergiebilanz bei Zusammenlagerung in einem Medium.
ΔG131 = ΔG11+ ΔG33- 2ΔG13
ΔG131 = -2(√γ1LW - √γ3LW)² - 4(√γ1+ - √γ3+)(√γ1- - √γ3-) [Gl.1.5.3]
-
Adhäsionsenergie zwischen Material 1 und Material 2 vermittels Fluid 3(ΔG132 ):
Grenzflächenenergiebilanz bei Zusammenlagerung unterschiedlicher Materie in einem Medium.
ΔG132 = ΔG12+ ΔG33- ΔG13- ΔG23
ΔG132 = -2(√γ1LW - √γ3LW)(√γ2LW - √γ3LW) + 2[(√γ1+ - √γ2+)(√γ1- - √γ2-) - (√γ1+ - √γ3+)(√γ1- - √γ3-) - (√γ2+ - √γ3+)(√γ2- - √γ3-)] [Gl.1.5.4]
Durch bestimmte Komponentenverhältnisse können ΔG131 , ΔG132 positive Werte annehmen. "Positiv" bedeutet, dem System müsste Energie zugeführt werden, der Vorgang liefe spontan nicht ab bzw. eben andersherum. ΔG > 0 bedeutet nichts anderes, als das Auftreten repulsiver (abstoßender) Kräfte. Für diese nicht-Adhäsion können verschiedene Szenarien formuliert werden, z.B. wenn in Situationen entsprechend Gl.1.5.4 folgende Relationen eintreten:
γ1LW < γ3LW< γ2LW und ggf. zusätzlich (√γ1- + √γ2-)> √γ3-
Anwendungsbeispiele: Mit Gl.1.5.2 wird erklärt, dass sich eine minimale Grenzflächenspannung zwischen Polymer und Additiv sehr positiv auf die Schlagzähigkeit des Kunststoffs auswirkt [95]. Mit Gl.1.5.3 wird erklärt, dass Ethylenglycol und Oktanol nicht mischbar sind [71, S.302]. Aus der Gl.1.5.4 wird abgeleitet, dass beim Einfrieren von biologischen Materialien in Glycerin Erythrozyten (rote Blutkörperchen) im zellulären Eis fixiert werden und dadurch nicht in der flüssigen Phase durch den osmotischen Druck zerstört würden [71, S.369].
1.7 Anwendungen im IMETER-Framework
Die Berechnungen aus Kontaktwinkel- und Komponentendaten werden im Framework für solide Körperoberflächen über METER M4 gegeben und für Messungen an porösen Materialien über IMETER M7 "PUK" Aus diesem Kontext stammen beispielsweise die automatisch erzeugten Diagramme 4, 5 und 6. Beide IMETER-Methoden sind für Oberflächenenergie-Messungen hochautomatisiert und mehr als einfach anwendbar. Man braucht nur Messungen durchzuführen und das Datenbaksystem stellt alle Kontaktwinkelergebnisse zu einer Probe zusammen und berechnet nach allen Verfahren (OWRK, Fowkes, OGC, Wu, Neumann) die Oberflächenenergie. Die Resultate werden grafisch präsentiert und tabellarisch gegenübergestellt. Und es werden zu jeder Berechnungsmethode Tabelle(n) herausgegeben die zeigen, welche Oberflächenenergie die Messdaten ergeben, wenn die einzelne Messung jeweils nicht im Ergebnis berücksichtigt wird. Das ist sehr praktisch, wenn man die Aufgabe ernst nimmt.
Andere Funktionen im IMETER-Framework liefern die Daten zu Ober- und Grenzflächenspannung (IMETER M1 und M2) und Viskosität und Dichte (IMETER M5, DiVA), so dass der ganze Themenkomplex vollständig mit einem Gerät bearbeitet werden kann.
2. Formeln zu Grenz- und Oberflächenspannung
2.1 Thermodynamische Grundlage
Vergrößert man eine Oberfläche um einen Betrag dA (alle anderen Quantitäten bleiben konstant), so ist dafür Energie aufzuwenden, d.h. die Arbeit dW mit dem Proportionalitätsfaktor γ, der Oberflächenspannung:
dW = γ·dA
Die zur Oberflächenbildung benötigte Arbeit leistet diesen Beitrag zur freien Enthalpie G. Für ein System mit veränderlicher Oberfläche im Zusammenhang mit den anderen thermodynamischen Quantitäten gilt: [3, 4]
dG = -S·dT + V·dp + γ·dA + Σµidni
Der Beitrag ist der selbe, der der freien Energie zukommt:
dF = -S·dT - p·dV + γ·dA + Σµidni
[G (Freie Enthalpie [G ≡ H -TS = U + pV -TS (Gibbs-Funktion), F (Freie Energie [F ≡ U -TS (Helmholtz-Funktion)]
Mit , innere Energie (U), Etnthalpie (H), Entropie (S) der Temperatur (T), Druck (p) und Volumen (V) und µi dem chemischen Potential der Komponente i mit der Teilchenzahl ni.
Man spricht Allgemein undifferenziert von der freien Oberflächenenergie (surface free energy).
-Nachfolgendes bedürfte der Überarbeitung-
2.2 (ältere) Berechnungsmöglichkeiten und Ansätze
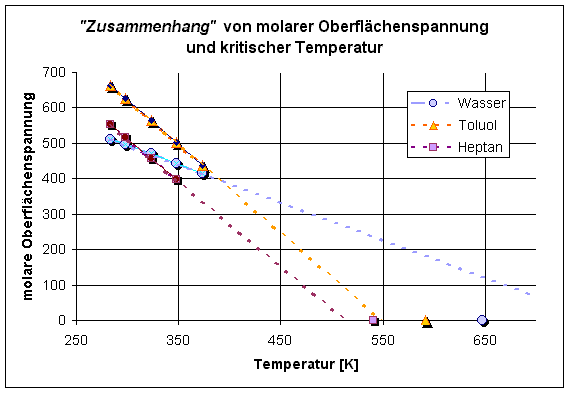
Molvolumen & Temperatur - Eötvös
Um die Oberflächenspannungen verschiedener Flüssigkeiten miteinander vergleichen zu können, wird die Oberflächenspannung molar normiert. Die Größe Vm2/3 (molares Volumen hoch 2/3) legt eine Fläche fest, die unabhängig von der Verbindung stets die gleiche Anzahl an Teilchen in der so definierten Mol-Oberfläche enthält, nämlich NL2/3(~ 7·1015 Teilchen). Die mit dieser Fläche multiplizierte Oberflächenspannung heißt dann molare Oberflächenspannung γm [mN/m ·(m3/mol)2/3]=[mJ·mol-2/3 ].
γm= γ·Vm2/3
Sie ist eine für den Vergleich verschiedener Stoffe geeignete Größe und stellt die Arbeit dar, die notwendig ist, um aus dem Innern der Flüssigkeit NL2/3Moleküle entgegen den zwischenmolekularen Anziehungskräften zur Oberfläche zu bringen.
Für viele normale Flüssigkeiten, d.h. nicht assoziierte Flüssigkeiten, gelte die Beziehung:
γm= kσ ·(TK' - T) (Eötvös´sche Regel)
TK' ist eine, ein wenig unter der kritischen Temperatur TK liegende Temperatur; T die betreffende Temperatur, die oberhalb der Mitte zwischen der absoluten Temperatur (0 K) und TK zu wählen ist. Die Gleichung wurde in Analogie zum allgemeinen Gasgesetz mit dem Theorem der übereinstimmenden Zustände hergeleitet. Der Temperaturkoeffizient kσ (T/dT) ist eine Konstante(Eötvös-Konstante, nach R. v. Eötvös 1848-1919)[98], sie sollte für normale Flüssigkeiten also stets den gleichen Wert haben: kσ = 2.1 [10-7 J·mol-2/3·K-1]. Der Wert gelte z.B. für Hg, CS2, CCl4, Nitrobenzol, Benzaldehyd. Abweichungen von diesem Wert deuten auf Assoziationen hin: Wasser 1.10, Ethanol 1.08, Aceton 1.82, Essigsäure 1.30, Phenol 1.36 (Werte von [22] S.395).
Das folgende Diagramm stellt für die drei darin bezeichneten Flüssigkeiten die Art des Zusammenhangs dar.
Es ist damit begreiflich, warum in neueren Lehrbüchern auf Eötvös meistens verzichtet wird. Die Regel hilft bzw. nützt kaum. Nach heutigem Verständnis ist die Assoziiertheit einer Flüssigkeit weitgehend aus der Strukturformel ersichtlich - für damals (1885) bei Fettsäuren (Essigsäure) aus den Daten der Oberflächenspannung. Doppelmoleküle, wie später durch andere Verfahren bestätigt, vorherzusagen, war gleichwohl eine respektable Leistung.
Molekülstruktur - Parachor
Die Oberflächenspannung einer Flüssigkeit ist bei gegebener Temperatur abhängig von der Differenz der Dichten der Flüssigkeit ρ und des Dampfes ρd. Nach D. M. MacLeod gelte dafür die Gleichung:
γ1/4 / (ρ-ρd) = k
Der Proportionalitätsfaktor k sei unabhängig von der Temperatur. S. Sugden erhielt nach Umformung mit der Molmasse M eine Größe, die er Parachor Pγ nannte.
P γ = M k1/4 = γ1/4 · M / (ρ-ρd)
Bei Temperaturen weit genug unter der kritischen kann die Dichte des Dampfes ρd vernachlässigt werden und mit M/ρ = Vm ergibt sich:
Pγ = Vm · γ1/4
Molekülparachore können aus der Summe der Atom- und Bindungsparachore berechnet werden und sollen auf Mischungen ebenfalls anwendbar sein.
Weitere Ansätze zur Berechnung
Über die Kohäsionsenergiedichte bzw. die Löslichkeitsparameter (Hildebrand, Hansen) werden folgende Gleichungen angegeben[6]:
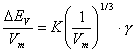 (Michaels)
(Michaels) 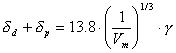 (Koehnen und Smolders)
(Koehnen und Smolders)
(ΔEV Verdampfungsenergie (ΔEV=ΔHV-RT); Vm Molvolumen; K eine Konstante; δp, δd Hildebrand-Parameter (δ=δd+δp+δh, entsprechend dispersen, polaren und Kräften und den Wasserstoff-Brücken))
In diesem Zusammenhang kann auch über parachorartige Bindungs- und Gruppeninkremente die Kohäsionsenergiedichte berechnet werden (Tabellen [25]).
2.3 Anreicherung an Grenzflächen, CMC
Moleküle mit eingebauter Zwiespältigkeit - hydrophil/hydrophob-Amphiphilie -, d.h. mit wasserfreundlichen und wasserunfreundlichen Molekülteilen, orientieren sich dementsprechend, dass polare (hydrophile) und unpolare (hydrophobe = lipophile) Teile sich nach Möglichkeit und entgegen dem Bestreben der Entropie zusammenlagern oder Stellen aufsuchen, die beiden Bedürfnissen gerecht werden. Solche Stellen können Oberflächen sein (die als Grenzflächen zum wechselwirkungsarmen Bereich zumindest keine abstoßenden Kräfte ausüben) oder Grenzflächen zu einer anderen kondensierten Phasen mit für einen Molekülteil besser passender Grenzflächenenergie. Bei fehlenden Grenzflächen bzw. genügender Konzentration (und geeigneter Konstitution) können sich diese Moleküle durch Zusammenlagerung selbst organisieren und Micellen*, Liposomen, Vesikel**, röhrenförmige, lamellare und andere Strukturen bilden (allg. Assoziationskolloide). Die Selbstorganisation ist eine überaus bedeutendes Verhalten. Man nimmt an, dass für die Ursprünge des Lebens eine so bewirkte Trennung von Innenwelt und Außenwelt - zu ersten, einfachen Zellen - notwendig war. Für Methoden der Nano-Technologie ist bedeutend, dass die Größenverteilung in einer mizellaren Lösung ziemlich gleich ist (homogen Monodispers), wodurch definierte Räume, z.B. als Bildungsmatrizen für den Aufbau anderer Moleküle oder Strukturen, vorliegen. Als Waschmittelrohstoffe (Tenside, Detergenzien), Emulgatoren, Dispersionsmittel, Katalysatoren (Phasen-Transfer-) Netzmittel, Verträglichkeitsvermittler, Antistatika in Kunststoffen, (Zell-)Membranbausteine u.s.w. haben grenzflächenaktive Substanzen eine herausragende Bedeutung.
*Micellen: (kolloidische) kugelförmige Zusammenballung von 20 bis 30 000 Molekülen. Für Na-Dodecylsulfat -Mizellen in Wasser wird die Zahl 70 angegeben. Typischerweise entspricht der Radius kugelförmiger Mizellen der statistisch geknäulten Länge des Moleküls. Die Größenverteilung der Mizellen ist normalerweise nahezu Monodispers. Mizellen und Monomere stehen in einem dynamischen Gleichgewicht. Bildungs- und Zerfallsgeschwindigkeites bewegen sich im Millisekunden-Bereich. Mizellen rotieren mit einer Frequenz in der Größenordnung von Nanosekunden.
**Vesikel: Begriff aus der Zytologie, bläschenförmige protoplasmatische Struktur mit einfacher Membran.
Lit.: [62], [67], [66], [68], [71], [84]
Die vordergründige Wirkung der Tenside besteht darin, in wässriger Lösung die Oberflächenspannung (Grenzflächenspannung) herabzusetzen. Aus diesem Grund ist die Tensiometrie ein besonders geeignetes Mittel zur Untersuchung und Charakterisierung dieser Stoffe über ihre Wirkung.Grenzflächenaktive Substanzen (auch Kunstwort Surfactants = surface active agents) haben typischerweise also einen zwittrigen Aufbau - d.h. Tensid oder Detergenz- Struktur. Der polare Teil (Kopf) der Moleküle kann je nach dem aus Carboxyl(at) (Fettsäuren, oder Salze), Hydroxyl (höhere Alkohole), Sulfon-, Sulfat-, Ammonium-, Amino- und Amidstrukturen wie aus Kombinationen Polyether-Alkohol, Betaine etc. gebildet werden. Funktionelle Gruppen also, die insbesondere Wasserstoff-Brücken bilden. Der lipophile Teil (Schwanz) kann in steigender Wirksamkeit aus Kohlenwasserstoff-, Dimethylsilikon-, (Per-) Fluorkohlenstoffketten aufgebaut sein.
Thermodynamik bis zum "CMC"
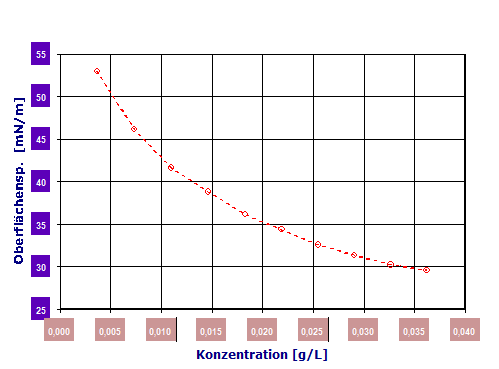
Fügt man man in kleinen Dosierungen "Tensid" einer Wasserprobe zu und misst dazu die Oberflächenspannung und trägt diese in einem Diagramm gegen die Tensidkonzentration ein, kann man einen Wirkungszusammenhang, wie in dem folgenden Diagramm erhalten:
Diagramm 2.3.1: Konzentrationsabhängigkeit der Oberflächenspannung. Der Zusammenhang ist stetig, doch nicht linear. (IMETER-Messung, Tensid: POLYDOCANOL, THESIT)
Die Substanz ist also sehr wirksam: 0.01g/L, entspricht 10mg pro Liter Wasser, verringert in diesem Fall die Oberflächenspannung bereits um 30mN/m.
(Der Messauflösung eines Tensiometers mit 0.01mN/m entspricht - in diesem Fall und Bereich - einem auflösbaren Konzentrationsunterschied von 3·10-6 g/L also 3µg/L bzw. 3mg pro Tonne [theoretisch])Thermodynamisch behandelt man die Grenzfläche als Zwischenraum, über den die Konzentration des Tensids sich sprunghaft ändert (Gibbs Dividing Surface).
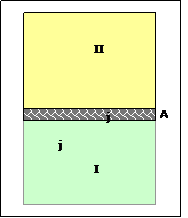
Die freie Enthalpie (G) eines zweiphasigen Systems besteht aus der Summe der Enthalpien der beiden Phasen (I und II) G=GI+GII
Die Anreicherung von Komponenten in der Grenzfläche führt dazu, dass G > GI+GII die gesamte freie Enthalpie größer ist, als diejenige, die sich aus der jeweiligen Verteilung der Komponente (j) auf die beiden Phasen ergibt – weil sich ein Teil in der Grenzfläche (A) anreichert. Die Grenzfläche gehört keiner Phase an.
G = GI+GII + GA (GA: freie Oberflächenenthalpie)
Die Summe der Tensid-Teilchen (nj) ist entsprechend auf die Phasen und die Grenzfläche verteilt:
nj = njI + njII+ njA in der Oberfläche also njA = nj – (njI + njII)
Die auf das Ausmaß der Oberfläche (A) bezogene Menge njA ist eine konstruierte Größe namens "Oberflächenüberschuss" (Γ), auch Oberflächenexzess genannt.
Γj = njA / ADie Fundamentalgleichung der chemischen Thermodynamik (mit Oberflächenterm):
isotherm (dT=0), isobar (dp=0) und im Gleichgewicht sind die chemischen Potentiale (µ) einer Komponente (j) in allen Phasen gleich (und dGA = dG - dGI - dGII):
Die Oberfläche (A) ändert sich nicht (dA=0) und nicht die Teilchenzahl (dnjA=0):
Bei konstantem Druck, Temperatur und Oberfläche ändert sich die freie Enthalpie nur mit der Zusammensetzung, die aber, wenn als konstant angesehen, wird zu dGA= 0.
mit (Γj = njA / A):
dγ ist der Abfall der Oberflächenspannung mit der Zunahme der Tensidkonzentration (Exzess) in der Oberfläche. Die Änderung der Oberflächenspannung entspricht der Änderung der Oberflächenkonzentration.
Im Beispiel mit nur einer Tensidart:
Mit dem chemischen Potential µ (Konzentration [Cj] = Aktivität (aj) bei verdünnten Lösungen)
folgt:
Γ entspricht der Geradensteigung, welcher also bezüglich der Konzentration ein logarithmischer Zusammenhang zugrunde liegen muss. - Das Diagramm 2.3.1 zeigte den ersten Teil einer CMC-Messung, wobei die X-Achse nicht-logarithmiert ist. Die Messung wurde weitergeführt und entsprechend Diagramm 2.3.2 auf logarithmischer X-Achse dargestellt:
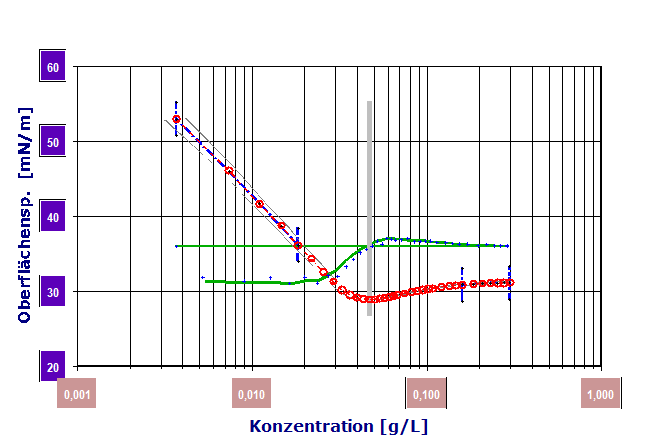
![022]() Diagramm 2.3.2: CMC Bestimmung (Differenzial-CMC mit IMETER) aus der Konzentrationsabhängigkeit der Oberflächenspannung. IMETER misst Daten und erzeugt dieses Diagramm automatisch. Die roten Marken stellen die Messwerte dar. Die grüne Linie ist der dazu gebildete Differenzenquotient - gibt also den anfangs ziemlich konstanten Wert von Γ wieder. In zahlreichen Messungen hat sich gezeigt, dass der Nulldurchgang des Quotienten von der Verfahrensgeschwindigkeit der Messung am wenigsten gestört wird. Der senkrechte, graue Balken markiert den CMC-Wert und die beiden blau markierten Bereiche sind der logarithmisch lineare Adsorptionsbereich (links) und der Sättigungsbereich (rechts). [(Tensid: (Wz.) POLYDOCANOL, THESIT, Lubrol PX, chemisch Dodecylpoly(ethylene-glycolether)n M ~583g/Mol]
Diagramm 2.3.2: CMC Bestimmung (Differenzial-CMC mit IMETER) aus der Konzentrationsabhängigkeit der Oberflächenspannung. IMETER misst Daten und erzeugt dieses Diagramm automatisch. Die roten Marken stellen die Messwerte dar. Die grüne Linie ist der dazu gebildete Differenzenquotient - gibt also den anfangs ziemlich konstanten Wert von Γ wieder. In zahlreichen Messungen hat sich gezeigt, dass der Nulldurchgang des Quotienten von der Verfahrensgeschwindigkeit der Messung am wenigsten gestört wird. Der senkrechte, graue Balken markiert den CMC-Wert und die beiden blau markierten Bereiche sind der logarithmisch lineare Adsorptionsbereich (links) und der Sättigungsbereich (rechts). [(Tensid: (Wz.) POLYDOCANOL, THESIT, Lubrol PX, chemisch Dodecylpoly(ethylene-glycolether)n M ~583g/Mol]
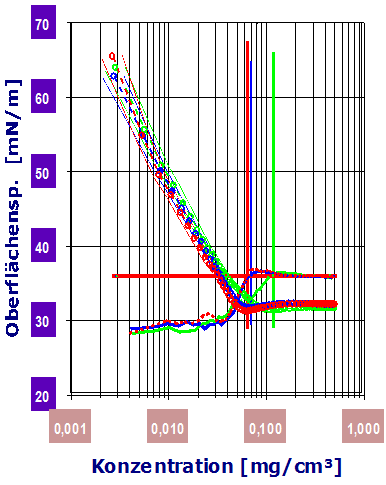
Wie im Diagramm gezeigt, kommt es ab etwa 0.025g/L zu einer Veränderung von Γ, bei ca. 0.05g/L tritt Γ=0 ein. Die Veränderung von Γ zeigt an, dass ab gewissen Konzentrationen sich die Aktivität (Konzentration) bzw. Teilchenzahl-Konzentrationsproportion ändert (Teilchenzahl ist nicht der Molzahl gleichzusetzen).Diagramm 2.3.4: IMETER Diagrammvergleich : Adsorptionsmessung durch Verschiebung der CMC: Messung ohne Zusatz (rot), mit 12 Gew.‑% Quarzsand (blau) und mit 3% Silicagel (grün). Das Silicagel adsorbiert größere Tensidmengen aus der Lösung, so dass dadurch die CMC (senkrechte Linie) zu doppelter Konzentration verschoben wird.
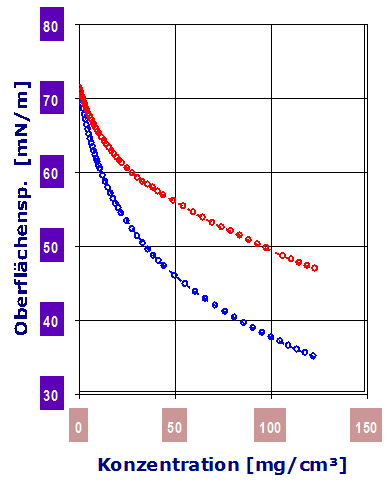
Der cmc-Wert wird nach der klassischen Methode aus dem Verlauf durch den Schnittpunkt der extrapolierten Geraden aus dem Adsorptions- und Sättigungsbereich berechnet. Dieses traditionelle Verfahren ist unsicher (vgl. Beispiel gealtertes Alkylsulfat - bei dem die Extrapolation unsinnig ist).Diagramm 2.3.5: IMETER Diagrammvergleich : Dosierung von 2-Propanol (blau) und Aceton (rot) in Wasser (bis 12%): 2‑Propanol ist zur Herabsetzung der Oberflächenspannung wirksamer.
Mit der Kinetik der Adsorption sind instationäre Diffusionsvorgänge verbunden (Gleichung von Ward und Tordai), die Adsorptionsvorgänge finden eine genauere Behandlung in den Ansätzen von Langmuir (auch Frumkin). Die Interaktion an Oberflächen ist nur ein Spezialfall der Grenzflächenbetrachtung, die Anreicherungen an festen oder flüssigen Grenzflächen sind nicht prinzipiell verschiedene Vorgänge.
Die Veränderung der Oberflächenspannung erfolgt durch grenzflächeninaktive Stoffe (z.B. anorganische Salze) derart, dass die Oberflächenspannung mit der Zugabe auch ansteigen kann.
2.4 Spreiten
Für unlösliche Moleküle, die auf eine Flüssigkeitsoberfläche aufgebracht werden, gilt im Idealfall (verdünnt, kein Volumen, keine Wechselwirkungen):
(γ° - γ)·A = k·T
Die Differenz γo-γ (Oberflächendruck) ist der Unterschied der Oberflächenspannung zwischen Flüssigkeit (Hypophase) und bedeckter Fläche A. A ist hier die Fläche, die ein Molekül einnimmt. Die Analogie mit dem allgemeinen Gasgesetz pV=nRT wird deutlich, wenn in obiger Gleichung die Bolzmann-konstante k=R/NL und 1mol/NL =n ersetzt wird: (γo-γ)Am=nRT. Somit ist der Oberflächendruck das zweidimensionale Analogon zum Gasdruck p und A die Entsprechung für Volumen. Die Fläche A (für ein Mol oder ein Molekül) kann so, d.h. unter gewissen Vorrausetzungen, zur Bestimmung von Molmassen bzw. Aggregierungsgraden herangezogen werden.
Der Ansatz ist im Prinzip auf einen bei noch geringeren Konzentrationen beginnenden Anfangsteil der Konzentrationsabhängigkeit der Oberflächenspannung (Diagramme oben, für nicht-ionische Tenside) anwendbar.

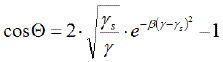
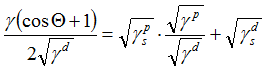 eine Geradengleichung, deren Steigung
eine Geradengleichung, deren Steigung 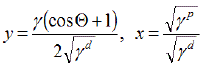 in ein Diagramm eingetragen:
in ein Diagramm eingetragen: