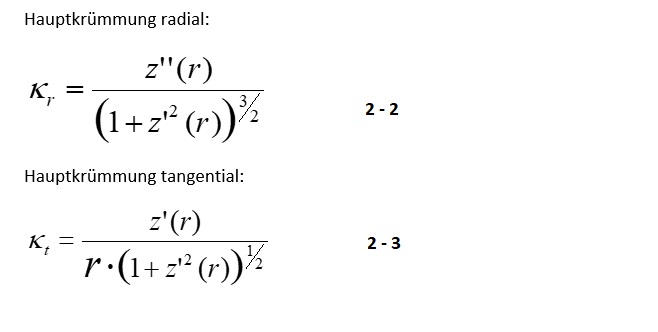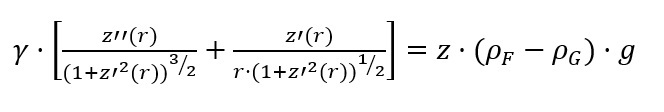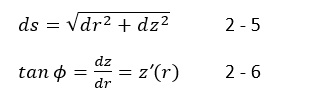IMETER -o- Ringmethode
I. Berechnung der Grenzflächenspannung aus Kraftmessungen an einem Ring
(IMETER- Ringmethode YLP)
von Thomas Petzoldt, M. Breitwieser (2014-2024)
Die Differentialgleichung zur Formulierung rotationssymmetrischer Grenzflächenkonturen wird hergeleitet, und als numerisches Verfahren angewendet.
Aufbau
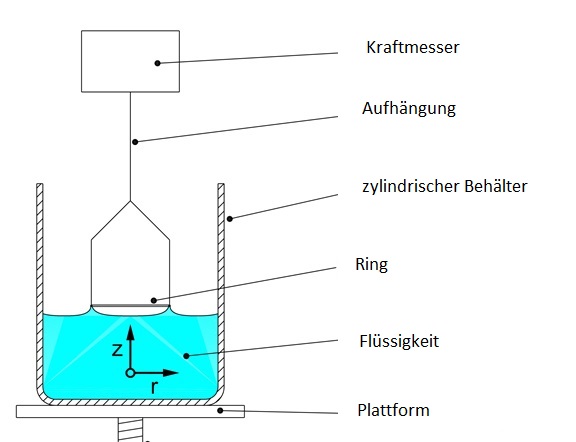 Abb.1 - schematischer Aufbau
Abb.1 - schematischer Aufbau
Formelzeichen: A Fläche [cm2]; α Winkel [rad]; d Differentialbezeichner; D Intervall / Differenz; g Ober- bzw. Grenzflächenspannung [mN/m]; F Kraft [mN]; j Konturwinkel [rad]; g Schwerebeschleunigung [m/sec2]; K Krümmung [1/mm]; p Druck [Pa]; r radiale Länge, Radius [mm]; R Hauptkrümmungsradius [mm]; r Dichte [g/cm3]; s Bogenlänge [mm]; Q Kontaktwinkel [rad]; z axiale Länge, Höhe [mm].
1 Kräftegleichgewicht am Flächenelement
Für die Druckkraft, die auf ein sphärisch gekrümmtes, infinitesimales Flächenelement wirkt, gilt (Abb. 2):
dF = Δp·dA 1-1
Mit den beiden Radien in Richtung der Hauptkrümmungen kann für das Flächenelement geschrieben werden:
dA = R1·dφ1· R2dφ2 1-2
Entgegen der Druckkraft wirkt die aus der Grenzflächenspannung resultierende Kraft in Normalenrichtung zum Flächenelement wie folgt:
dF = γ· (R1·dφ1 · 2sin(dφ2/2) + R2·dφ2 · 2sin(dφ1/2)) 1-3
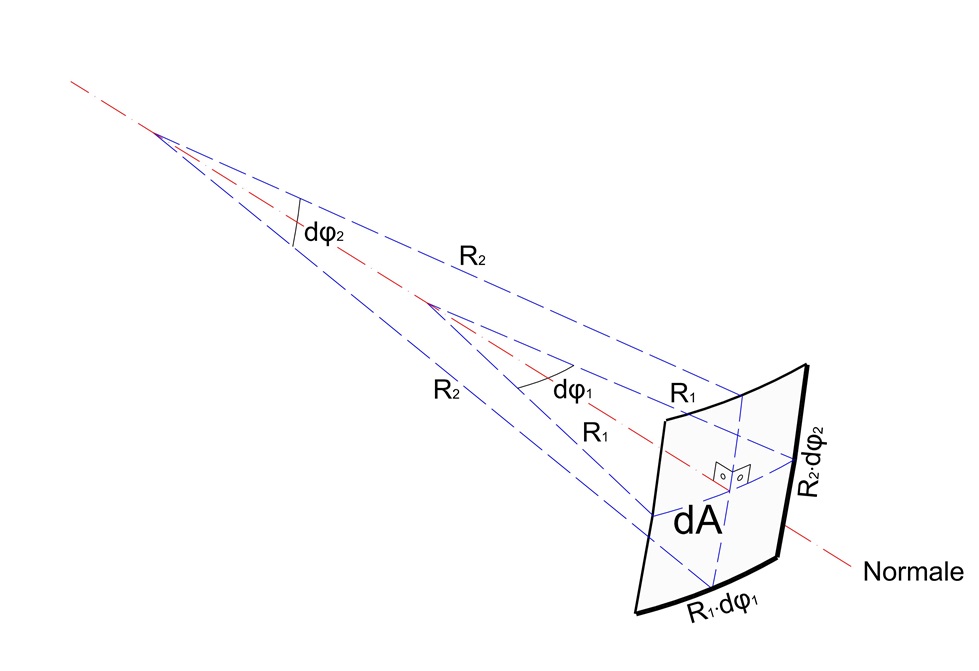 Abb. 2
Abb. 2
Mit der Vereinfachung für infinitesimal kleine Winkel
2sin(dφ/2) = dφ 1-4
können die beiden Kräfte ins Gleichgewicht gesetzt werden, wobei sich die Winkeltherme herauskürzen.
γ· (R1 + R2) = Δp·R1·R2 1-5
Die erhaltene direkte Beziehung zwischen Grenzflächenspannung und örtlicher Druckdifferenz wird mit den Krümmungen als Kehrwert des Krümmungsradius ausgedrückt.
K1 = 1/R1 ; K2 = 1/R2 1-6
γ·(K1 + K2) = Δp 1-7
Der Ausdruck 1-7 entspricht der Young-Laplace-Gleichung. Das Produkt beider Krümmungen in Hauptkrümmungsrichtung wird auch als Gauß’sche Krümmung bezeichnet.
2 Differentialgleichung der Grenzflächenkontur
Die hydrostatische Druckdifferenz zwischen den beiden Phasen ist eine Funktion der Steighöhe z.
Δp = (z - z0)·(ρF - ρG)·g 2-1
Die Höhenkoordinate z0, bei der die Druckdifferenz zu Null wird, soll fortan zu Null gesetzt werden (Nullniveau).
Die Kontur der Grenzfläche bei der Messung mit der Ringmethode ist rotationssymmetrisch. Daraus folgt, dass die Ausrichtung der beiden Hauptkrümmungen an jeder Position radial/tangential ist.
Durch Einsetzen der Gleichungen 2-1, 2-2 und 2-3 in Gleichung 1-7 erhält man als Differentialgleichung mit der radialen Konturfunktion z(r):
Obwohl Gleichung 2-4 relativ unhandlich erscheint, kann mit den geeigneten Umformungen und dem Setzen von Startbedingungen ein numerisches Ergebnis iterativ erzielt werden.
Für die Bogenlänge s und den Steigungswinkel φ der Konturfunktion gilt:
Damit wird aus den Krümmungen
Kr = dφ / ds 2 -7
Kt = sinφ / r 2 -8
und in Gleichung 2 -4 eingesetzt.
γ·(dφ/ds + sin(φ)/r) = z·(ρF - ρG)·g 2-9
3 Numerische Berechnung der Grenzflächenkontur
Zunächst wird Gleichung 4-9 wie folgt umgeformt:
dφ/ds = z·(ρF - ρG)·g/γ - sin(φ)/r 3 - 1
Die Wahl einer hinreichend kleinen Diskretisierungsschrittweite Ds stellt bei der üblichen Rechenleistung heutiger Computer kein Problem mehr dar. Mit dem Festlegen zutreffender Anfangswerte rAnf, zAnf und φAnf ergibt sich der weitere Verlauf der Kontur aus den jeweils vorhergehenden Werten.
ri+1 = ri + Δs · cos φi 3 - 2
zi+1 = zi + Δs · sin φi 3 - 3
Zur Nachbildung der Lamellenkontur aus dem Versuchsaufbau in Kapitel 1. wird zunächst die innere Grenzfläche berechnet. Ausgehend von der Symmetrieachse gilt:
Der Parameter zAnf wird dann solange variiert, bis die Konturkurve tangential innen an dem Drahtring anliegt (Abb. 3).
Die Anfangswerte für die äußere Grenzfläche ergeben sich aus der Randbedingung, dass die Konturkurve tangential außen am Drahtring anliegen muss. Dabei wird φAnf zum Iterationsparameter wodurch sich mit der Randbedingung rAnf und zAnf ergeben. Durch die Iteration wird dann φAnf so bestimmt, dass die Konturkurve die Behälterwand mit dem vorgegebenen Kontaktwinkel schneidet (Abb. 3).
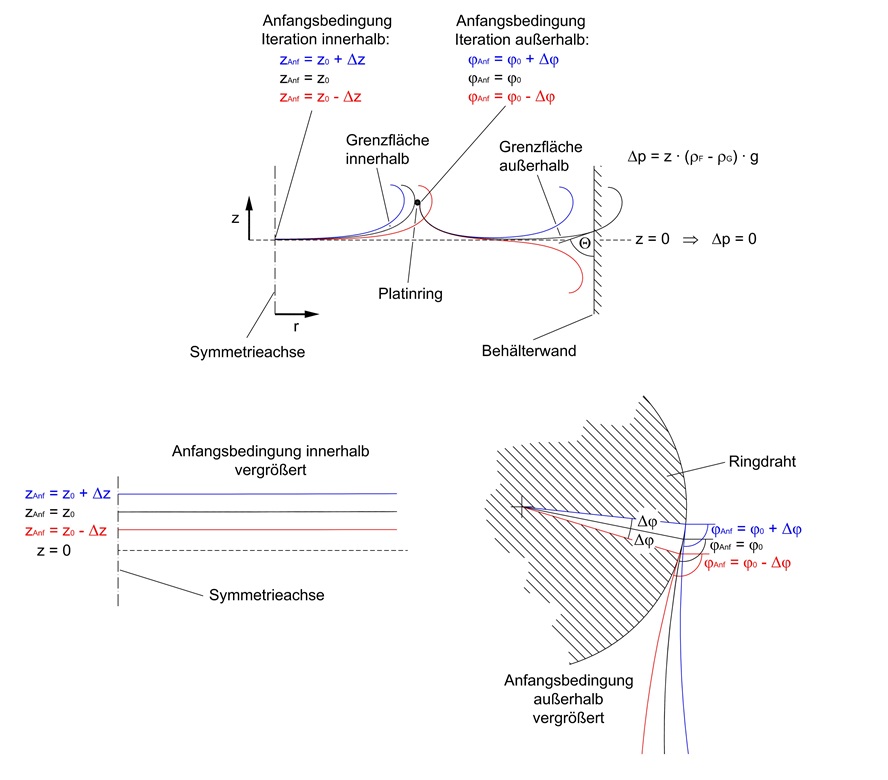
Abbildung 3
4 Berechnung der Kraft am Ring
Nachdem die Kontur der Grenzfläche bekannt ist, muss die resultierende Gesamtkraft am Ring bestimmt werden. Diese addiert sich aus drei Bestandteilen (Abb. 4).
Fγa = γ·2π· ra · cos αa 4 - 2
Integration der örtlichen Druckdifferenz über den Ringumfang und das benetzte Drahtsegment.
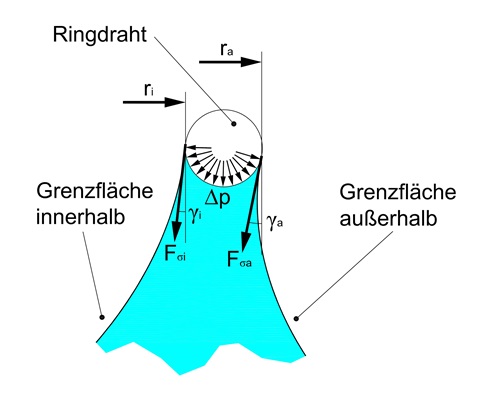
Abbildung 4
Abb. 5 zeigt beispielhaft einen mit dem beschriebenen Verfahren berechneten Weg-Kraft Verlauf.
Abbildung 5
5 Berechnung der Grenzflächenspannung aus der Maximalkraft
Die vorstehenden Kapitel 2. bis 6. beschreiben die Berechnung von Grenzflächenkontur und Kraft bei gegebener Ausziehhöhe des Rings sowie bekanntem Verhältnis der Dichtedifferenz zur Grenzflächenspannung.
Für die praktische Anwendung im IMETER Verfahren ist es aber erforderlich bei bekannter Dichtedifferenz und Maximalkraft die sich daraus ergebende Grenzflächenspannung zu ermitteln.
Dazu werden mehrere Iterationsschleifen ineinander verschachtelt:
.