Wilhelmy-A (M12)
Description given with the Program:
Das IMPro ist relativ umfangreich, weil eine ziemlich vollständige Fehlerfortpflanzung (weitgehend nach GUM) durchgeführt wird und die Ergebnisse ausführlich formatiert werden.
Wilhelmy-A beginnt mit einem Startmenü über das Probenname, Messtemperatur, Anzahl Einzelmessungen und andere Einstellungen (Justierung, Rührwerk) vorgewählt werden.
Im IMPro wird der folgende Ablauf ausgeführt:
- Waage prüfen / Justieren, Atmosphärendaten aufzeichnen.
- Rührwerk prüfen / einregeln, Rühren.
- Temperierung prüfen / einregeln.
- Wilhelmyplatte - konditionieren und einsetzen.
- Temperaturmessen, Rührer aus.
- Oberfläche annähern, Platte Vortauchen, zurück auf Kontakthöhe und Benetzungskraft messen
- Platte zurückziehen, Rührer an, Temperatur messen
- Wiederholungen (4. - 7.)
- Ende, Bericht.
- Wilhelmy-Platte mit Aufhänger: Es muss nicht unbedingt eine Platinplatte sein. Für organische Flüssigkeiten kann eine dünne Glasscheibe etwa ein Deckgläschen verwendet werden.
- Probengefäß: Am besten das Standardtemperiergefäß mit Deckel verwenden. Gleichwohl kann ggf. ein einfacher Behälter mit hinreichendem Durchmesser (>2x Plattenbreite) verwendet werden, wenn bei Präzision und Richtigkeit gewisse Abstriche hingenommen werden können.
- Das IMPro verwendet I-Magnetrührer bzw. die Vorgängerversion des Rührgerätes, falls angeschlossen. Wenn das Rührgerät nicht vorhanden ist, wäre das fürs IMPro auch kein Problem.
- Die Temperierung wird überwacht - eine Temperaturregelung findet jedoch nicht statt. Natürlich muss der Temperaturfühler in der Probe stecken.
Das Programm ist auf die Messung niederviskoser Flüssigkeiten eingestellt und funktioniert im Temperaturbereich zwischen 10 bis 40°C. Höhere Viskosität, Dampfdruck, Temperatur können durch Anpassungen der Parameter wahrscheinlich auch gemessen werden.
*ToDo: tx-Strings in Berichtselemente einfügen - zur Tabellenformatierung.
General hints: The Source Code of an IMETER measurement program (IMPro) consists of a sequence of statements that are executed line by line. To make the IMPro easier to understand, different elements are highlighted in the source code below:
Commands, IF-Conditions, Loops and Line-Jumps, Defining Variables, Calculations, ⌨Variables that create a Menu item at Start-up (☞or latent menu items), External Component Action (⎙accessory, ☋closer and ☏farther devices), Comments and Hints, Info Messages, User Interaction or Input(☝). - Titles of Sub-Programs: SUB Program ,MENU-COMMAND - accessible by Toolbar/Menu during execution, AUTO-SUB - as periodic self-calling program part. The '•' or '#SubProgramName' means call of the SubProgram; Appearances of '@' denoting inline evaluations within a Text fragment. Some of the statements are pre-evaluated by the interpreter and can modify the representations in the data form, request additional information (for configuration) as well as the menu of the toolbar and the user interface during the run.
MAIN PROGRAM - Wilhelmy-A - V.7.2.54 - Apr 9 2019
- #Start
- #Messung
- ƒ Berichtsausgabe: - generates each time a new line of entries to the table -
Messung der Oberflächenspannung durch die Wilhelmy-Methode
Probenbezeichung: @Probenbezeichnung@
Es wurden @LfNr_@ unabhängige Bestimmungen durchgeführt.
@Zusammenfassung@
Die Tabelle zeigt formal das Ergebnis für die ermittelte Messgröße (Y). Der Eintrag y(x) gibt den Wert, uc(y)rel., uc(y) die relative und absolute kombinierte Standardmessunsicherheit, U0,95 und U0,99 sind die erweiterten Standardmessunsicherheiten für die Überdeckungswahrscheinlichkeit von 95% und 99%.
- ƒ DatenblattOptionen: Methode = Massebestimmung : 58ÿ8/0// 9/1/@Probenbezeichnung@ / 18/1/@OFS__##3@±@uc(OFS)##3@mN·m-1 /24/1/@STemp * (2* LfNr_ )^(-1) ##2@ Setting Evaluation method and changing visibility or entries in the selected data field(s).
- #Schluss
1a —×— SUB —×— ———————————————Start———————————————————————————————
2a ——— '0. Probendaten angeben - Parameter der Messung' ———————————————————
3a »»» [TEXT *] Probenbezeichnung = !Seifenlösung Nr.4 (!Seifenlösung Nr.4 ) Bitte geben Sie die Bezeichnung der Probe an
4a ⌨ [Zahlenangabe *] nGesamtdurchgänge (?3 n) Zahl der Einzlmessungen.
5a »»» *Rührwerk_verwenden = 'nein/aus' (?Yes) Wenn deaktiviert - wird weder i-Magnetrührer noch der io-Rührer angesteuert.
6a ⌨ [Number *] DrehzahlStart (?10 n) Wirksam, wenn i-Magnetrürer verfügbar -- Die Rührerdrehzahl - Umwälzen, nicht schäumen!
7a »»» *Temperatur_regeln = 'nein/aus' (?No) Wenn deaktiviert - findet keine Regelung statt und es wird einfach bei der vorliegender Temperatur gemes...
8a ⌨ [Temperature *] Ziel_Temperatur (?25 °C) Die Probentemperatur zur Messung - bei Temperaturgradientenmessung ist hier z.B. die Maximaltemperatur anzugeben!
9a ⌨ [Temperature *] TemperaturToleranz (?0,1 °C) Die Genauigkeit mit der die Messtemperatur erreicht sein muss.
10a ⌨ *NurTemperiertMessen (?No) Wenn aktiviert wird nur in der Temperaturgrenze gemessen!
11a ⌨ [Time *] maxGGWartezeit (?120 s) Zeit die maximal auf einen Kraftendwert gewartet wird! - Achtung bei hoher Viskosität ggf. in Minutenbereiche heraufsetzen!
12a ⌨ [Absolute height *] Plattenumfang (?@2*(0,215+19,95)*exp(( Ziel_Temperatur - 25 )* 8,8E-6 )#2@ mm) Die Platte - Allgemein Umfang ⇒ 2·l + 2·b oder pi·d. Mit Berücksichtigung der Wärmedehnung 8,8 E-6/K für Platin!
13a ⌨ [Absolute height *] uPlattenumfang (?0,15 mm) Messunsicherheit der Plattendimension.
14a [Mass/Weight] "WZReproduzierbarkeit" = 0,0001 [g] .. Konstante der Wägezelle bzw. Berücksichtigung der Umstände beim Methodeneinsatz - als praktische Reproduzierbarkeit
15a »»» *Justierung_der_Wägezelle = 'ja/an' (?No) Wenn aktiviert wird - bei Bedarf - die Justierung der Waage durchgeführt.
16a ⌨ [y/n] Messung_der_Luftdichte (?No) Wenn aktiviert wird die Luftdichte bestimmt (wenn I-SIF da, automatisch, sonst Angabe von Lufttemperatur, -Feuchte und -Druck im Dialog erforderlich).
17a [TEXT] "RhoL_und_WZKalibrierzustand" = Textvariable mit '' initiieren
19a ——— 'Waage prüfen / Justieren, Atmosphärendaten -' —————————————————————
20a [Textvariable] "RhoL_und_WZKalibrierzustand" = @ @
21a #Luftdichte und WZ-Justierung sicherstellen
22a ——— 'Rührwerk prüfen / einregeln, Rühren -' —————————————————————————
23a IF "Rührwerk_verwenden" THEN: #Rührwerk Konfigurieren und anschalten
24a ——— 'Temperierung prüfen / einregeln-' ———————————————————————————
25a IF "Temperatur_regeln" THEN: #Temperierung sicherstellen
- ═══════════════════════════════════════════#Start•|
1b —×— SUB —×— ———————————————Messung—————————————————————————————
2b ——— 'ggf. Positionieren ...' —————————————————————————————————
3b [Textvariable] "Zusammenfassung" = Y Symbol Unit y(x) uc(y) uc(y)rel. U0,95 U0,99
4b [Zahlenangabe] "LfNr_" = 0 [n]
5b [Textvariable] "MeldungstexT1" =
Und mit den Bewegtasten zur Oberfläche "fahren" ...
6b JUMP 4 Lines forward
7b [136] [137]
8b ØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØ
9b [Textvariable] "MeldungstexT1" =
OK.
10b [6] IF "Rührwerk_verwenden" THEN: • Rührer einschalten
11b IF "Temperatur_regeln" THEN: #Temperierung sicherstellen
12b Stage light: active
13b CALL USER: 'Jetzt bitte soll nur der Adapter für die Wilhelmyplatte am Lastträger einhängen. Quittieren. Während dessen die Wilhemyplatte reinigen, dest. Wasser abspülen und kurz ganz wenig "rotglühen" ...'
Confirmation: Keyboard or IMETER
14b #WZ Stillstand abwarten
15b WEIGHING CELL: Tare
16b IF "Rührwerk_verwenden" THEN: • Rührer ausschalten
17b CALL USER: 'Bitte jetzt die Wilhelmyplatte zur @LfNr_ +1#@. Messung von "@Probenbezeichnung@" am Wägeadapter einhängen. @MeldungstexT1@'
Confirmation: Keyboard or IMETER
18b Z-MOVE: 10,000 mm DOWN v= 5,00 mm/s
19b Stage light: off
20b ——— '@LfNr_ +1@. Wägung der Platte' ———————————————————————————
21b #WZ Stillstand abwarten
22b LfNrT = 0 -- Bestimmung des genauen Tarawertes
23b Sum_T = 0
24b ²Sum_T = 0
25b -a- Wägewert [g] = W ⇒ liest den Wägewert - d.h. die Anzeige der Waage
26b -|- LfNrT = LfNrT + 1
27b -|- Sum_T [g] = Sum_T + Wägewert summation
28b -|- ²Sum_T = ²Sum_T +( Wägewert )^2 Quadratsumme ...
29b -|- Wait: 0,005 s
30b -a- LOOP: 5 lines back, 50× repetition • • • • • • • • • • • • • • • • • • • • • •
31b FORCE: 1-times
32b MW_Tara [g] = Sum_T / LfNrT
33b StdAbw_Tara [g] = SQR(ABS(1/( LfNrT -1)* ( ²Sum_T - ( Sum_T ^2 / LfNrT )))) ... ABS weil manchmal quadratsumme ganz wenig k...
35b IF "Rührwerk_verwenden" THEN: • Rührer einschalten
36b -b- Wait: 5 s
37b -|- IF "Rührwerk_verwenden" THEN: • Rühr-Richtung Wechseln
38b -|- IF "Temperatur_regeln" THEN: #Temperierung sicherstellen
39b -b- LOOP: 3 lines back, 1× repetition • • • • • • • • • • • • • • • • • • • • • •
40b [Temperaturangabe] "Temperatur1" = T [°C]
41b Record Temperature
42b IF "Rührwerk_verwenden" THEN: • Rührer ausschalten
43b Z-MOVE: 10,000 mm UP v= 5,00 mm/s
45b IF "LfNr_ =0" THEN: 4 Lines forward
46b [Absolute Höhe] "Starthöhe" = Kontakthöhe - 1 [mm]
47b Z-MOVE: ⇳ "Starthöhe" v= 5,00 mm/s
48b Wait: 0,300 s
49b [45] LfNr_ [n] = LfNr_ + 1
50b ——— '@LfNr_ @. Messung ...' ———————————————————————————————
51b [54] Z-MOVE: 0,035 mm UP v= 0,300 mm/s
52b LOOP: one line back, max.750-times OR UNTIL "|dW|>1,5 mg" IS TRUE
53b IF "last loop regular finished" THEN: Message (Stop): Ist Probe im Gefäß - oder die Platte zu weit von der Oberfläche?
54b IF "last loop regular finished" THEN: 3 Lines backward
55b Z-MOVE: 0,075 mm DOWN v= 0,500 mm/s
56b [Absolute Höhe] "Kontakthöhe" = H [mm]
57b [rel. Bewegstrecke] "BenetzungsStrecke" = 3 [mm-rel]
58b Z-MOVE: ⇳ "BenetzungsStrecke" v= 2,50 mm/s
59b Wait: 7,500 s
60b [rel. Bewegstrecke] "BenetzungsStrecke" = - BenetzungsStrecke [mm-rel]
61b Z-MOVE: ⇳ "BenetzungsStrecke" v= 2,50 mm/s
62b ggZeit = t
63b #WZ Stillstand abwarten
64b ggZeit = t - ggZeit
66b LfNrW [n] = 0
67b Sum_W = 0
68b ²Sum_W = 0
69b -c- Wägewert [g] = W - MW_Tara ABZUG VON TARA !!
70b -|- LfNrW = LfNrW + 1
71b -|- Sum_W = Sum_W + Wägewert summation
72b -|- ²Sum_W = ²Sum_W +( Wägewert )^2 Quadratsumme ...
73b -|- Wait: 0,005 s
74b -c- LOOP: 5 lines back, 50× repetition • • • • • • • • • • • • • • • • • • • • • •
75b FORCE: 1-times
76b Z-MOVE: 4,000 mm DOWN v= 2,50 mm/s
77b IF "NOT Rührwerk_verwenden" THEN: 4 Lines forward
78b • Rührer einschalten
79b Wait: 3 s
80b • Rühr-Richtung Wechseln
81b [77] Wait: 4 s
82b Record Temperature
83b [Temperaturangabe] "Temperatur2" = T [°C]
84b Z-MOVE: 11,000 mm DOWN v= 5,00 mm/s
86b ——— '⇒Achtung Gauss <> GUM --- Stdabw. und Stdabw des Mittelwertes!' ———————————
87b MW_Messung [g] = Sum_W / LfNrW
88b uNettoW [g] = SQR(ABS(1/( LfNrW -1)* ( ²Sum_W - ( Sum_W ^2 / LfNrW ))))
89b Linearitätsfehler [g] = W''' *( MW_Messung )/ 50 proportionale approx.
90b IF "MW_Messung >50 [g]" DEFINE: 'Linearitätsfehler = W''' [g]'
91b u_WZKalibE2 [g] = MW_Messung /200 *0,0003 Kalibriergewicht Klasse E2 - pro 100g, 0,15mg max. Unsicherheit
92b k_WZTempKoeff [g] = MW_Messung * 1E-6 * WZcT Temperaturkoeffizient: 1E-6/K
93b u_Wägung [g] = SQR( WZReproduzierbarkeit ^2 + Linearitätsfehler ^2 + StdAbw_Tara ^2 + uNettoW ^2 + k_WZTempKoeff ^2 + u_WZKalibE2 ^2) ...
95b ƒ Berichtsausgabe: - generates each time a new line of entries to the table -
- Datenprotokolle, Dokumentation
- Tabelle 1: Zusammenfassung der Ergebnisdaten -
Die Tabelle gibt mit T die Temperatur der Probe als Mittelwert vor und nach der Messung an. Mit γ wird der Schätzwert zur Oberflächenspannung gegeben. Die Zeit - bzw. Geschwindigkeit - für die Einstellung der Messkraft zum statischen Endwert ist mit tGG angegeben, H° ist die Niveauhöhe der Probenoberfläche in der Skala des Platformniveaus vom IMETER.
Nr° T[°C] γ[mN/m] tGG[s] H°[mm]
@LfNr_@. @( Temperatur1 + Temperatur2 )/2 ##2@ @MW_Messung * g / ( Plattenumfang * 0,001)##3@ @ggZeit##1@ @Kontakthöhe@
96b ƒ Create Report: - generates each time a new line of entries to the table -
- Tabelle 2: Protokoll der Wägungen -
Die Tabelle gibt mit (t) den relativen Zeitpunkt des einzelnen Messwertes wider. WTara ist das Gewicht der Platte vor dem Flüssigkeitskontakt und mit Wbrutto in Kontakt mit der Probe. Die zugehörigen Standardabweichungen (Stichproben) aus je @LfNrW - 1@Wägungen sind mit ±σ bezeichnet.
Nr° t[min] WTara[g] ±σ[g] Wbrutto[g] ±σ[g]
@LfNr_@. @TIMR##1@ @MW_Tara##5@ @StdAbw_Tara##5@ @MW_Messung + MW_Tara##5@ @uNettoW##5@
97b ——— '⇒Standardmessunsicherheit und Freiheitsgrade' ————————————————————
98b Linearitätsfehler [g] = Linearitätsfehler / SQR(3) 'Linearitätsfehlers' der Waage mit Gewichtung 'Rechteck'
99b [Massen-/Gewichtsangabe] "u_Tara" = 0 [g]
100b u_Tara [g] = SQR(1/( LfNrT *( LfNrT -1))* ( ²Sum_T - ( Sum_T ^2 / LfNrT ))) emp. Stdabw. d. MW (Typ A) zur Standardme...
101b JUMP 2 Lines forward
102b u_Tara [g] = SQR(ABS(1/( LfNrT -1 ) * ( ²Sum_T - ( Sum_T ^2 / LfNrT )))) Stdabw!
103b [101] u_WProbe [g] = SQR(1/( LfNrW *( LfNrW -1))* ( ²Sum_W - ( Sum_W ^2 / LfNrW )))
104b JUMP 2 Lines forward
105b u_WProbe [g] = SQR(ABS(1/( LfNrW -1)* ( ²Sum_W - ( Sum_W ^2 / LfNrW )))) -> Stichproben Stdabw
106b [104]
107b u_Wägung [g] = SQR( WZReproduzierbarkeit ^2 + Linearitätsfehler ^2 + u_Tara ^2 + u_WProbe ^2 + k_WZTempKoeff ^2 + u_WZKalibE2 ^2) ...
108b u_WProbe [g] = SQR(1/( LfNrW *( LfNrW -1))* ( ²Sum_W - ( Sum_W ^2 / LfNrW )))
109b S_uc_Wägung [g] = S_uc_Wägung + u_Wägung Summierung für Durchschnittsangabe
110b u_Wägung [g] = u_Wägung Format5 Ausgabewert auf 5 Stellen gerundet
111b Testrechnung [n] = ((( u_Tara )^4/( LfNrT -1))+ (( u_WProbe )^4/( LfNrW -1))) Nenner = 0?
112b IF "Testrechnung <>0" DEFINE: 'FG_effWägung = u_Wägung ^4 / Testrechnung [g]'
113b IF "FG_effWägung =0" THEN: Message (Stop): Null Freiheitsgrade!?
114b FG_effWägung [n] = FG_effWägung Format0 Rundung auf Ganzzahl
115b DEFINE : 'FG_effWägungTXT = FG_effWägung [TEXT]'
116b IF " FG_effWägung >999 [n]" DEFINE: 'FG_effWägungTXT = >100 [TEXT]'
118b [Zuweisung n] "FGeff" = FG_effWägung
119b [Zuweisung g] "YWert" = MW_Messung
120b [Zuweisung g] "uc(Y)" = u_Wägung
121b [Zahlenangabe] "NaKoSte" = 5 [n]
122b [Textvariable] "YBezeichnung" = Wbrutto - WTara mW@LfNr_@ g
123b #k95-k99
125b ——— 'Summationen zur Statistik' ——————————————————————————————
126b STemp [°C] = STemp + Temperatur1 + Temperatur2 summation
127b ²STemp [°C] = ²STemp + ( Temperatur1 + Temperatur2 )^2 summation
128b SumNetto [g] = SumNetto + MW_Messung summation
129b ²SumNetto = ²SumNetto + ( MW_Messung )^2 Quadratsumme ...
130b IF "LfNr_ <2 [n]" THEN: 4 Lines forward
131b StdAbw_Temp [°C] = SQR(ABS(1/( LfNr_ -1)* ( ²STemp - ( STemp ^2 / LfNr_ ))))
132b uNettoW [g] = SQR(ABS(1/( LfNr_ *( LfNr_ -1))* ( ²SumNetto - ( SumNetto ^2 / LfNr_ )))) Stdabw. des Mittelwertes!
133b MWNetto [g] = SumNetto / LfNr_
134b [130]
135b ——— 'weitere Messung ...' —————————————————————————————————
136b IF "LfNr_ < nGesamtdurchgänge" THEN: 129 Lines backward
137b QUESTION '@LfNr_ +1@. Durchlauf - Messprozedur jetzt beenden?' IF No ⇒ 130 Lines backward
138b ØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØØ
140b IF "Rührwerk_verwenden" THEN: • Rührer ausschalten
141b [Textvariable] "Zusammenfassung" = @Zusammenfassung@
142b ƒ Berichtsausgabe: - generates each time a new line of entries to the table -
- Tabelle 3: Messunsicherheiten der als Wägung ausgeführten Benetzungs-Kraftmessungen -
@Zusammenfassung@
143b ƒ Berichtsausgabe: - generates each time a new line of entries to the table -
----- Ausführliche Erläuterung für den @LfNr_@. Messdurchgang ----
Die Bestimmung der Standardmessunsicherheit der Massebestimmung per Waage (uW) berücksichtigt folgende Unsicherheitsbeiträge:
- u(W0) : Unsicherheit des Nullpunktes =@1000* u_Tara#mg#2@ berücksichtigt die vorliegenden Bedingungen als Schwankung des Tarawertes vor der Messung (Typ A).
- u(W1) : Unsicherheit der Wägung =@1000* u_WProbe#mg#2@ reflektiert die Schwankungen des Wägewertes bei der Messung (Typ A).
- u(s) : Reproduzierbarkeit =@1000* WZReproduzierbarkeit#mg#2@ ist eine Datenblattangabe der Sartorius-Wägezelle - als Standardabweichung (Typ B, Normalverteilung).
- u(Lin) : Linearitätsunsicherheit = @1000* Linearitätsfehler#mg#2@ ist Präzisionsmaß der Waage nach Datenblatt - an den Wägebereich angepasst (Typ B, Rechteckverteilung, Halbbreite @1000* Linearitätsfehler * SQR(3)#mg#2@).
- u(TK) : temperaturbedingte Abweichung= @1000* k_WZTempKoeff#mg#2@ - Durch den Temperaturunterschied zw. Kalibrierung und Messung wird der Temperaturkoeffizient wirksam, er beträgt 1 ppm/K. Die Temperaturabweichung wird ggf. korrigiert, aber zugleich als Unsicherheitsbetrag gewertet (Typ B, Normalverteilung).
- u(mcal) : max.Kalibrierabweichung = @1000* u_WZKalibE2#mg#2@ ist die Unsicherheit der Kalibrierung gemäß der Klasse des Justiergewichts: OIML Klasse E2 entspricht 1,5ppm. (Typ B, Normalverteilung).
Es wird die Unterflurwägung angewendet, daher wird ein Exzentrizitätsfehler nicht gesetzt. Die Eingangsgrößen sind nicht korreliert, zudem gilt ∂ƒ/∂Xi = ci =1. Damit wird die kombinierte Standardmessunsicherheit der Wägung angegeben mit:
uc(W) = √(u²(s) +u²(W0) + u²(W1) + u²(Lin) + u²(TK) + u²(mcal))
Die kombinierte Standardmessunsicherheit der Wägung beträgt @1000* u_Wägung#mg#2@. Die Zahl der effektiven Freiheitsgrade (νeff.) wird zu @FG_effWägungTXT#@ bestimmt. @txtErweiterungsfaktor@
mm@LfNr_@ =@YWert##5@ g ±@uc(Y)##5@ g.
145b uc(MASSE) [g] = S_uc_Wägung / LfNr_
146b uFallbeschl [m/s²] = g * 0,0001
147b OFS__ [mN/m] = g * MWNetto /( Plattenumfang *0,001)
148b c_OFS_m [1/s²] = g /( Plattenumfang * 0,001) Sensitivitätskoeffizient
149b c_OFS_dm [1/s²] = c_OFS_m Sensitivitätskoeffizient
150b c_OFS_g [g/m] = - MWNetto /( Plattenumfang *0,001) Sensitivitätskoeffizient
151b c_OFS_L [g/ms²] = - g * MWNetto /( Plattenumfang *0,001)^2 Sensitivitätskoeffizient
152b uc(OFS) [mN/m] = SQR( ( c_OFS_m * uNettoW )^2 + ( c_OFS_dm * uc(MASSE) )^2 + ( c_OFS_L * uPlattenumfang *0,001)^2 + ( c_OFS_g * uFallbeschl )^2)
153b relative_uc(OFS) [%] = 100* uc(OFS) / OFS__
154b FG_effOFS [n] = uc(OFS) ^4 /((( uc(MASSE) )^4/( LfNr_ -1 ))+ ( uNettoW ^4 /( LfNr_ -1 )) ) Format0 Zahl der effektiven Freihei...
155b [Zuweisung n] "FGeff" = FG_effOFS
156b [Zuweisung mN/m] "YWert" = OFS__
157b [Zuweisung mN/m] "uc(Y)" = uc(OFS)
158b [Zahlenangabe] "NaKoSte" = 3 [n]
159b [Textvariable] "YBezeichnung" = Oberfl.spannung γW mN/m
160b [Textvariable] "Zusammenfassung" = Y Symbol Unit y(x) uc(y) uc(y)rel. U0,95 U0,99
161b #k95-k99
162b JUMP 2 Lines forward
163b [Textvariable] "Zusammenfassung" = @Zusammenfassung@
164b [162] uc(MASSE) [g] = uc(MASSE) Format4 formatierung
165b ƒ Create Report: - generates each time a new line of entries to the table -
III. Vollständiges Ergebnis zur Messung der Oberflächenspannung
Auswertungsmodell:
γW = FM / PPlatte = ( mM + δm ) · g / (2·lPlatte + 2·bPlatte)
Die Oberflächenspannung gemäß der Wilhemymethode γW ergibt sich aus der Benetzungskraft (FM) bei vollständiger Benetzung (Kontaktwinkel 0) aus dem Verhältnis zur benetzten Länge, d.h. dem Umfang P. Die Kraft wird auf der Waage formal als Masse (m) gemessen. Der Ausdruck δm steht für die mittlere Streuung der Wägewerte (der Wert ist '0'). Mit der lokalen Fallbeschleunigung (g) erhält man mit F = m·g die Kraft. Der Umfang der Platte @Plattenumfang#mm#2@ entspricht der benetzte Länge (2×Länge ×Breite, bei der Temperatur @Ziel_Temperatur#°C@) .
Die Messunsicherheit der Oberflächenspannung wird aus der Standardmessunsicherheit der @LfNr_@Messungen mit um =@uNettoW#g#5@ und dem Mittelwert der kombinierten Standardmessunsicherheiten der Massebestimmungen uδ =@uc(MASSE)#g#5@ sowie den als normalverteilt behandelten Unsicherheiten bezüglich des Plattenumfangs uP = @uPlattenumfang@ und der Unsicherheit über die lokale Fallbeschleunigung ug= @g * 0,0001#m/s²#5@ abgeleitet.
Xi xi u(xi) ci ci·u(xi)[mN/m] νi
mM [g] @MWNetto##5@ @uNettoW##5@ @c_OFS_m##-5@ [1/s²] @ c_OFS_m * uNettoW ##5@ @LfNr_ - 1#@
δm [g] 0 @uc(MASSE)##5@ @c_OFS_dm##-5@ [1/s²] @ c_OFS_dm * uc(MASSE)##5@ @FG_effWägungTXT#@
PPlatte[m] @Plattenumfang * 0,001##5@ @uPlattenumfang *0,001##5@ @c_OFS_L##-5@ [g/ms²] @ c_OFS_L * uPlattenumfang *0,001##5@ ∞
g [m/s²] @g *1@ @g * 0,0001##5@ @c_OFS_g##-5@ [g/m] @c_OFS_g * uFallbeschl ##5@ ∞
γW @OFS__##3@ [mN/m] u(y)=√(∑(ci·u(xi))²)= @uc(OFS)##3@ νeff @FG_effTXT#@
Die kombinierte Standardmessunsicherheit beträgt @uc(OFS)#mN/m#4@.
@txtErweiterungsfaktor@
Die erweiterte Messungsicherheit U beträgt @k(95) * uc(OFS)#g/cm³#4@. Sie ist das Produkt der erweiterten Standardmessungsicherheit mit dem Erweiterungsfaktor k=@k(95)@ und stellt bei Normalverteilung die Überdeckungswahrscheinlichkeit von 95% dar (U bei k=@k(95)@, P=95%).
Oberflächenspannung von @Probenbezeichnung@ wird für die Temperatur @STemp / (2* LfNr_ )##2@°C ± @StdAbw_Temp##2@°C zu @OFS__##3@ mN/m ±@k(95) * uc(OFS)##3@ mN/m ermittelt, die relative Messunsicherheit beträgt ±@k(95) * relative_uc(OFS)##-3@%.
e--167. ══════════════════════════════════════════ #Messung•|
1c —×— SUB —×— ———————————————Luftdichte und WZ-Justierung sicherstellen———————————————
2c IF "NOT Messung_der_Luftdichte" THEN: 5 Lines forward
3c Record density of Air
4c LuftDichte [kg/m³] = rhoL /1000
5c [Textvariable] "RhoL_und_WZKalibrierzustand" = @RhoL_und_WZKalibrierzustand@ Die Luftdichte beträgt @LuftDichte@ (Zeitpunkt @TIME@).
6c JUMP 5 Lines forward
7c [2] LuftDichte [kg/m³] = rhoL /1000
8c [Textvariable] "RhoL_und_WZKalibrierzustand" = @RhoL_und_WZKalibrierzustand@ Die Luftdichte beträgt gemäß Konfiguration @LuftDichte#g/cm³@.
10c IF "NOT Justierung_der_Wägezelle" THEN: 22 Lines forward
11c [6] [Textvariable] "RhoL_und_WZKalibrierzustand" = @RhoL_und_WZKalibrierzustand@. Die Temperatur an der Wägezelle beträgt @WZaT#°C@.
12c ——— '*** Ob die automatische Justierung erforderlich ist (1x täglich, und bei Temp.änderung >1K) ***' —
13c IF "ABS( WZcT )>1 [K]" THEN: 5 Lines forward
14c IF " WZct >24 [h]" THEN: 4 Lines forward
15c [Textvariable] "RhoL_und_WZKalibrierzustand" = @RhoL_und_WZKalibrierzustand@ Der Kalibrierzustand der Wägezelle wurde überprüft: letztmalige Justage vor @WZct#@ Stunden bei @WZaT - WZcT##1@°C.
16c JUMP 19 Lines forward
17c ——— '*** Sichere Justierung - Vorprüfung auf Stillstand ***' ———————————————————
18c [13] [14] [28] Stage light: active
19c Accustic signal: ♪
20c QUESTION 'Bitte evtl. vorhandene Lasten / Wägeadapter von der Waage nehmen, weil die Waage jetzt justiert werden muss. Diese Meldung (mit Ja) quittieren, sobald bereit.' IF No ⇒ 14 Lines forward
21c Stage light: off
22c Wait: 0,500 s
23c LOOP: one line back, max.15-times OR UNTIL "dF=0 mN" IS TRUE
24c WEIGHING CELL: Tare
25c Wait: 0,300 s
26c LOOP: one line back, max.15-times OR UNTIL "|W|>0,2 mg" IS TRUE
27c IF "last loop regular finished" THEN: 2 Lines forward
28c JUMP 10 Lines backward
29c [27] WEIGHING CELL: Adjust
30c [Textvariable] "RhoL_und_WZKalibrierzustand" = @RhoL_und_WZKalibrierzustand@ Die Wägezelle wurde zur Messung um @TIME@ justiert.
32c [10] IF "NOT Justierung_der_Wägezelle" AND "NOT Messung_der_Luftdichte" THEN: 3 Lines forward
33c ƒ Berichtsausgabe: - generates each time a new line of entries to the table -
Jusierung der Waage, Luftdichtebestimmung
@RhoL_und_WZKalibrierzustand@
34c [20] Stage light: off
- [16] [32] ════════════════════════════════════════#Luftdichte und WZ-Justierung sicherstellen•|
1d —×— SUB —×— ———————————————WZ Stillstand abwarten———————————————————————
2d [Zeitangabe] "timec" = t [s]
3d [9] Wait: 0,150 s
4d LOOP: one line back, max.100-times OR UNTIL "dW=0 mg" IS TRUE
5d Wait: 0,300 s
6d LOOP: one line back, max.10-times OR UNTIL "|DW|>0,15 mg" IS TRUE
7d IF "last loop regular finished" THEN: 3 Lines forward
8d IF "t - timec > maxGGWartezeit " THEN: #Warnsignal
9d IF "t - timec < maxGGWartezeit " THEN: 6 Lines backward
10d [7]
- ═════════════════════════════════════════ #WZ Stillstand abwarten••|
1e —×— SUB —×— ———————————————Warnsignal—————————————————————————————
2e Stage light: toggle
3e Accustic signal: ♪
4e Stage light: toggle
- ══════════════════════════════════════════ #Warnsignal•|
1f —÷— MENU-COMMAND —÷— ————————| Unterbrechung - ein gewisse Zeit pausieren |—————————————
2f ☝ [Zeitangabe *] "Pausendauer" Geben Sie bitte eine Zeit in Sekunden an, während der das Programm hier - z.B. zum Temperieren - anhält!
3f Enable Menu
4f Wait: ⌚ "Pausendauer"
- ════════════════════════════════════════ • Unterbrechung - ein gewisse Zeit pausieren•|
1g —×— SUB —×— ———————————————Temperierung sicherstellen——————————————————————
2g [7] IF "ABS( T - Ziel_Temperatur ) - TemperaturToleranz >0 [°C]" THEN: #Warnsignal
3g -d- • Rühr-Richtung Wechseln
4g -|- IF "NOT NurTemperiertMessen" THEN: 5 Lines forward
5g -|- Wait: 3 s
6g -d- LOOP: 3 lines back, max.3-times OR UNTIL "ABS( T - Ziel_Temperatur ) - TemperaturToleranz <=0 °C" IS TRUE
7g IF "ABS( T - Ziel_Temperatur ) - TemperaturToleranz >0 [°C]" THEN: 5 Lines backward
- [4] ═════════════════════════════════════════#Temperierung sicherstellen••|
1h —×— SUB —×— ———————————————Rührwerk Konfigurieren und anschalten————————————————
2h "iMagnetrührer" = 'nein/aus'
3h IF "i-Stirrer 'connected' " DEFINE: 'iMagnetrührer = 1 [j/n]'
4h IF "NOT iMagnetrührer" THEN: 5 Lines forward
5h ☞ [Number] Drehzahl = DrehzahlStart [n] Wirksam, wenn i-Magnetrürer verfügbar -- Die Rührerdrehzahl - Umwälzen, nicht schäumen!
6h ⎙ i-Stirrer: Turn on
7h ⎙ i-Stirrer: Speed: "Speed"
8h JUMP 2 Lines forward
9h [4] • Rührer einschalten
- [8] ════════════════════════════════════════ #Rührwerk Konfigurieren und anschalten•|
1i —÷— MENU-COMMAND —÷— ————————| Rührer einschalten |————————————————————————
2i IF "iMagnetrührer" THEN: 3 Lines forward
3i IDA-Out: active
4i JUMP 2 Lines forward
5i [2] ⎙ i-Stirrer: Turn on
- [4] ══════════════════════════════════════════• Rührer einschalten••|
1j —÷— MENU-COMMAND —÷— ————————| Rühr-Richtung Wechseln |—————————————————————
2j IF "iMagnetrührer" THEN: 3 Lines forward
3j IDA-Out: toggle
4j JUMP 2 Lines forward
5j [2] ⎙ i-Stirrer: Change Direction
- [4] ═════════════════════════════════════════ • Rühr-Richtung Wechseln••|
1k —÷— MENU-COMMAND —÷— ————————| Rührer ausschalten |———————————————————————
2k IF "iMagnetrührer" THEN: 4 Lines forward
3k IDA-Out: off
4k IDA-Out: off
5k JUMP 2 Lines forward
6k [2] ⎙ i-Stirrer: Turn off
- [5] ═════════════════════════════════════════ • Rührer ausschalten••|
1l —÷— MENU-COMMAND —÷— ————————| Rühr-Geschwindigkeit Ändern |———————————————————
2l IF "iMagnetrührer" THEN: 5 Lines forward
3l IDA-Out: active
4l DIALOG: '... Stellen Sie bitte jetzt am Drehknopf des Rührwerks die passende Geschwindigkeit ein.'
Confirmation: Keyboard or IMETER
5l IDA-Out: off
6l JUMP 4 Lines forward
7l [2] IF "iMagnetrührer" THEN: • Rührer einschalten
8l ☝ [Zahlenangabe *] "Drehzahl" Aktuell ist die Drehzahl auf @Drehzahl@% gesetzt.... Geben Sie bitte ggf. einen passenden Wert ...
9l ⎙ i-Stirrer: Speed: "Speed"
- [6] ═════════════════════════════════════════• Rühr-Geschwindigkeit Ändern••|
1m —×— SUB —×— AUTO 0,65sec———————————————Blinken———————————————————————
2m Start thread Processes
3m Stage light: toggle
- ═══════════════════════════════════════════#Blinken•|
1n —×— SUB —×— ———————————————k95-k99——————————————————————————————
2n IF " FGeff >999 [n]" DEFINE: 'FG_effTXT = >100 [TEXT]'
3n IF " FGeff <999 [n]" DEFINE: 'FG_effTXT = FG_eff [TEXT]'
4n IF " FGeff =0" THEN: 6 Lines forward
5n k(95) [n] = -0,55527/( FGeff ^5) + 5,9127/( FGeff ^4) - 0,46960/( FGeff ^3) + 3,5389/( FGeff ^2) + 2,3231/ FGeff + 1,9601
6n k(99) [n] = 48,799/( FGeff ^5) - 24,813/( FGeff ^4) + 25,338/( FGeff ^3) + 6,7041/( FGeff ^2) + 5,0582/ FGeff + 2,5737
7n [Textvariable] "txtErweiterungsfaktor" = Erweiterungsfaktoren k0,95 = @k(95)@, k0,99 = @k(99)@.
8n [Textvariable] "txt_U(Y95-99)" = @k(95) * uc(Y)##NaKoSte@ @k(99) * uc(Y)##NaKoSte@
9n JUMP 3 Lines forward
10n [4] [Textvariable] "txt_U(Y95-99)" =
11n [Text] "txtErweiterungsfaktor" = _
12n [9] IF "YWert <>0" DEFINE: 'Yrel_uc = 100*ABS( uc(Y) / YWert ) [%]'
13n IF "YWert =0" DEFINE: 'Yrel_uc = xxx [j]'
14n [Textvariable] "Zusammenfassung" = @Zusammenfassung@
@YBezeichnung@ @YWert##NaKoSte@ @uc(Y)##NaKoSte@ @Yrel_uc#@% @txt_U(Y95-99)@
- ══════════════════════════════════════════ #k95-k99•|
1o —×— SUB —×— ———————————————Schluss——————————————————————————————
2o ƒ Create Report: - generates each time a new line of entries to the table -
Anmerkungen
JCGM 100:2008 (GUM) fordert ein Modell für die Auswertung anzuwenden, das alle eingehenden Größen behandelt. Die Zahl der effektiven Freiheitsgrade (νeff) wird für die Wägungen nach der Welch-Satterthwaite-Formel berechnet und angegeben. Und hat dementsprechende Auswirkung auf den Wert des Erweiterungsfaktors k zur Intervallangabe der Überdeckungswahrscheinlichkeit von 95% und 99% (k0,95 bzw. k0,99). Die Interpretation der Freiheitsgrade bei der Angabe für die Wägungen - als unabhängige Einzelinformation - ist nicht unstrittig. -- Dieser automatisierte Bericht formatiert Stellenangaben (Anzahl der Nachkommastellen) nicht immer korrekt. Die intern 16-stelligen Berechnungen können bei der Überprüfung zu geringen Abweichungen durch Rundungseffekte führen.
3o #Blinken
4o IF "Rührwerk_verwenden" THEN: • Rührer ausschalten
5o DIALOG: 'Die Messung ist beendet !' Confirmation: Keyboard or IMETER
6o Stop thread Processes
7o Stage light: off
- ═══════════════════════════════════════════#Schluss•|
|
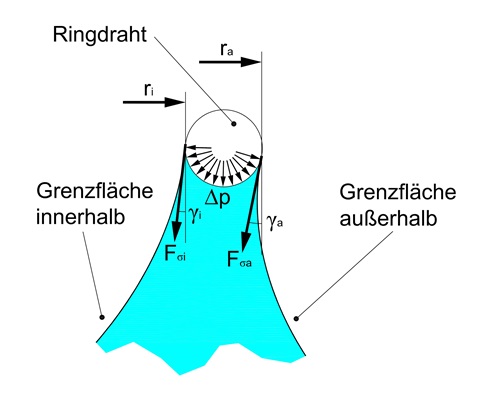
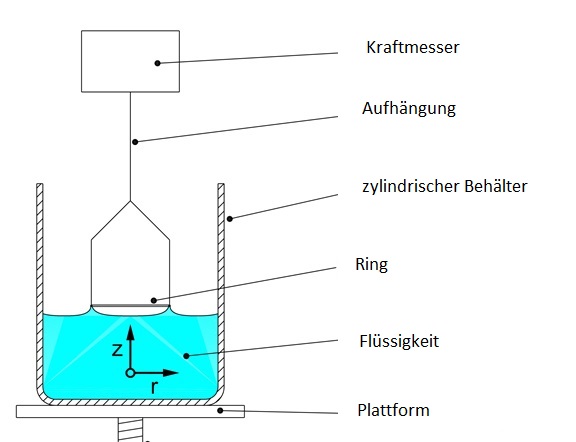
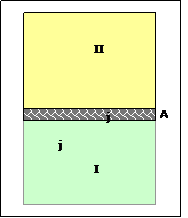
![]() Abb.1 - schematischer Aufbau
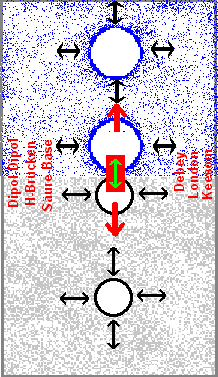
Abb.1 - schematischer Aufbau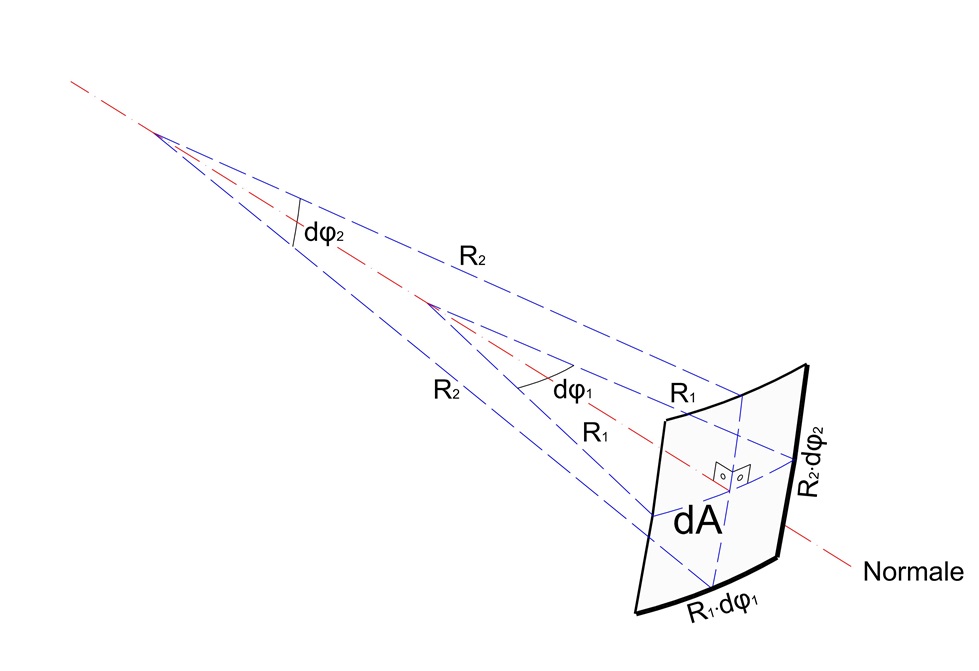 Abb. 2
Abb. 2 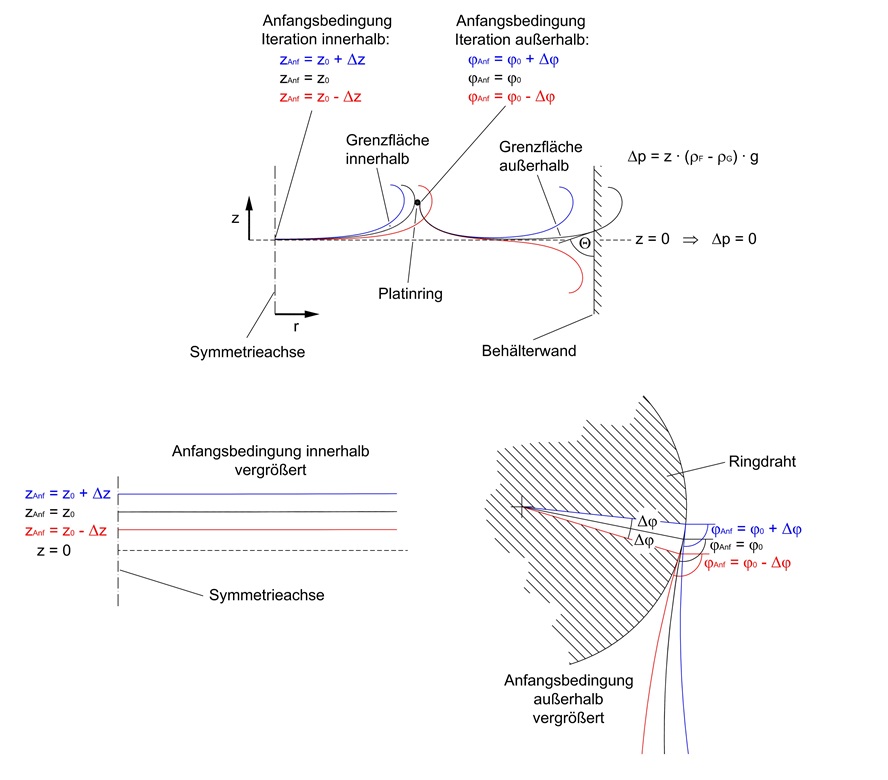

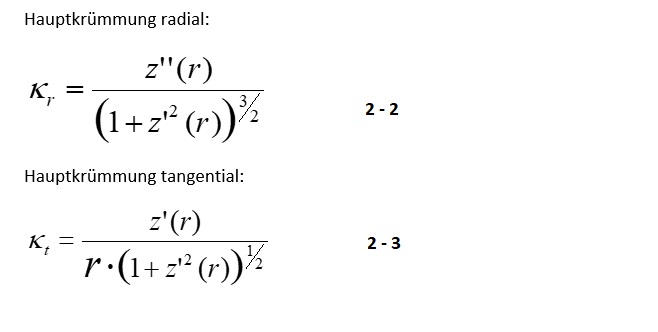
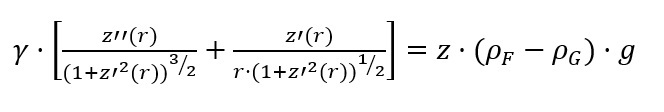

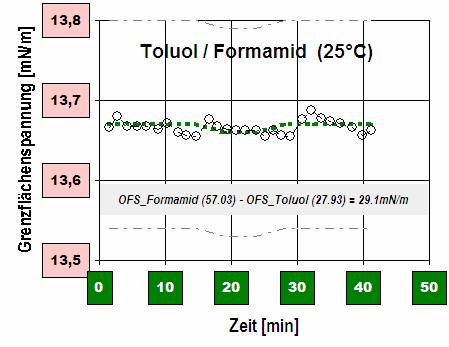
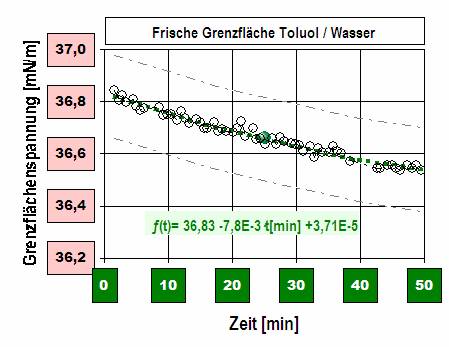
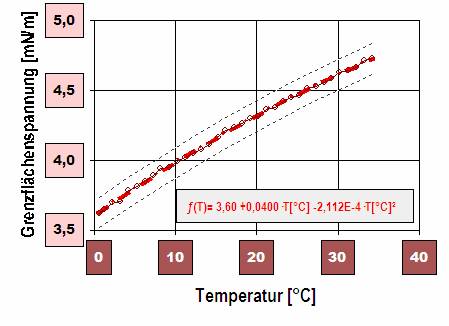
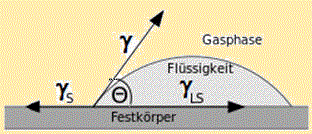 berflächenspannung von Flüssigkeiten der direkten Messung zugänglich ist, nämlich durch die Bestimmung der Kraft, die der Erzeugung neuer Oberfläche entgegensteht, ist die Oberflächenspannung fester Körper praktisch nur indirekt messbar. Die Oberflächenspannung charakterisiert die einzelne Flüssigkeit. Sie bestimmt beispielsweise die freie Tropfenform und -größe oder auch den Druck in Gasblasen (Hohlräumen). Zwischen nichtmischbaren flüssigen Phasen ist die Stabilität beider Phasen jeweilig von der adhäsiv wirkenden Grenzflächenspannung und der kohäsiven Oberflächenspannungen der Einzelflüssigkeiten abhängig. Bei Benetzung und Benetzbarkeit der Wechselwirkung flüssiger und fester Stoffe sind die Verhältnisse der Ober- und Grenzflächenspannungen der hier nun beteiligten drei Phasen in Betracht zu ziehen. Bei Feststoffen erzeugt der Begriff 'Oberflächenspannung' Verwirrung, weil diese mechanische Spannung nicht so unmittelbar erkennbar ist - bei fester Materie ist es darum üblich, den allgemeinen Begriff Oberflächenenergie zu verwenden.
berflächenspannung von Flüssigkeiten der direkten Messung zugänglich ist, nämlich durch die Bestimmung der Kraft, die der Erzeugung neuer Oberfläche entgegensteht, ist die Oberflächenspannung fester Körper praktisch nur indirekt messbar. Die Oberflächenspannung charakterisiert die einzelne Flüssigkeit. Sie bestimmt beispielsweise die freie Tropfenform und -größe oder auch den Druck in Gasblasen (Hohlräumen). Zwischen nichtmischbaren flüssigen Phasen ist die Stabilität beider Phasen jeweilig von der adhäsiv wirkenden Grenzflächenspannung und der kohäsiven Oberflächenspannungen der Einzelflüssigkeiten abhängig. Bei Benetzung und Benetzbarkeit der Wechselwirkung flüssiger und fester Stoffe sind die Verhältnisse der Ober- und Grenzflächenspannungen der hier nun beteiligten drei Phasen in Betracht zu ziehen. Bei Feststoffen erzeugt der Begriff 'Oberflächenspannung' Verwirrung, weil diese mechanische Spannung nicht so unmittelbar erkennbar ist - bei fester Materie ist es darum üblich, den allgemeinen Begriff Oberflächenenergie zu verwenden. [Gl.1.3.6]
[Gl.1.3.6]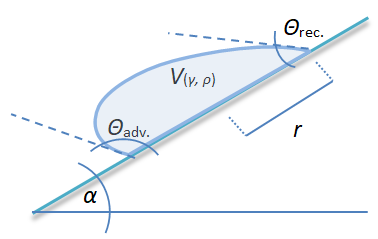 Der Fall von Fluidbrücken in einer Kapillare ist physikalisch gut beschreibbar. Mathematisch und messtechnisch erheblich schwieriger ist die Modellierung für liegende Tropfen (Bild rechts), wobei deren Praxisbezug vielfach gegeben ist. Quéré [Lit.
Der Fall von Fluidbrücken in einer Kapillare ist physikalisch gut beschreibbar. Mathematisch und messtechnisch erheblich schwieriger ist die Modellierung für liegende Tropfen (Bild rechts), wobei deren Praxisbezug vielfach gegeben ist. Quéré [Lit. 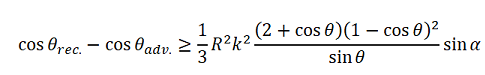 [
[
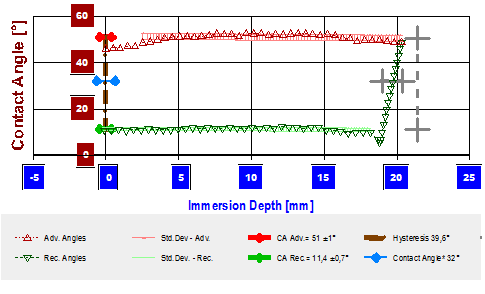
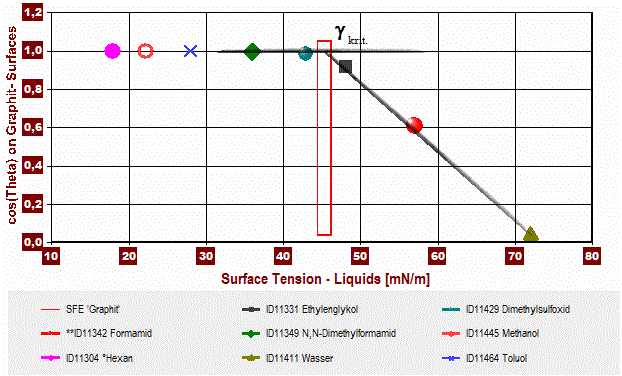
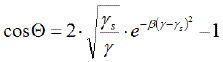
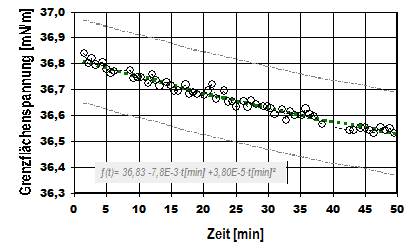
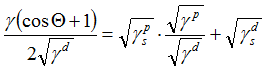 eine Geradengleichung, deren Steigung
eine Geradengleichung, deren Steigung 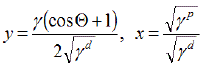 in ein Diagramm eingetragen:
in ein Diagramm eingetragen: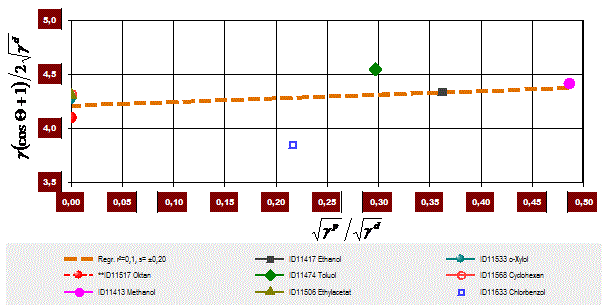
![Benetzungsdiagramm, Wetting-Zones (Wetting-Envelop) für ein spezielles Glas [IMETER 11637] Wetting Alkaliglas](https://imeter.de/images/ART/M7/Wetting_Alkaliglas.gif)
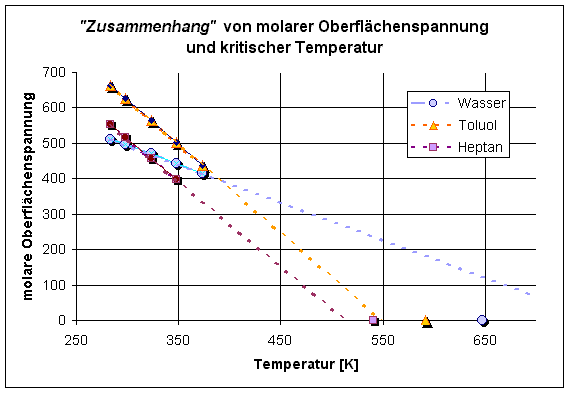
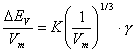 (Michaels)
(Michaels) 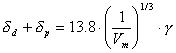 (Koehnen und Smolders)
(Koehnen und Smolders)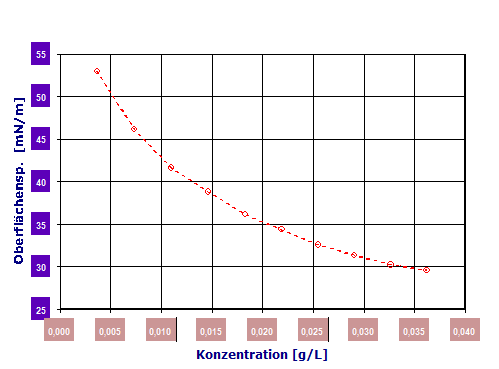
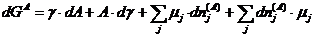
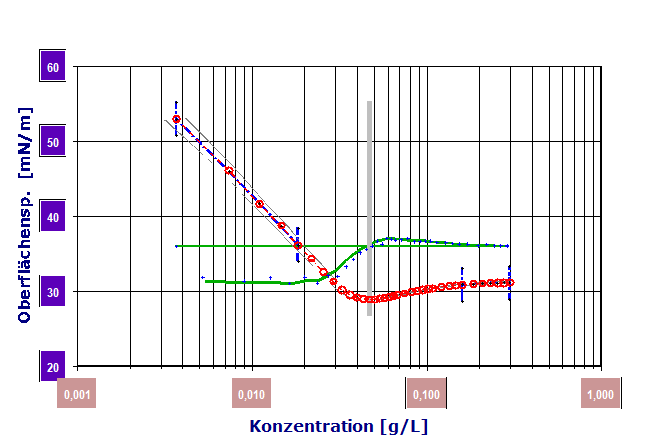
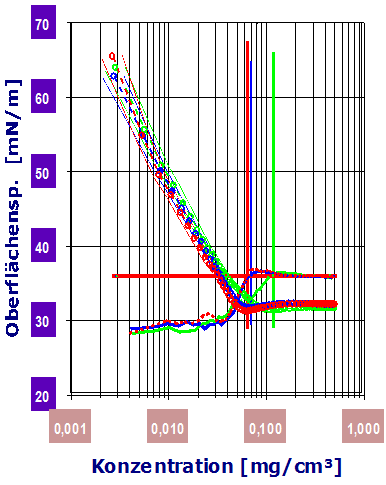
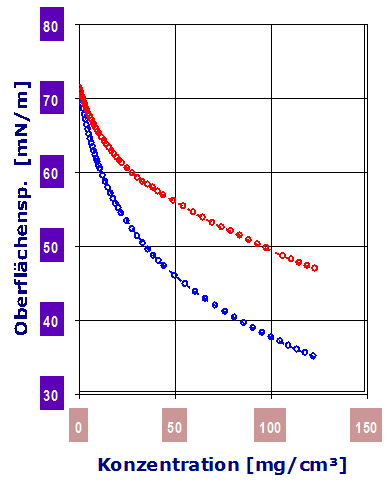
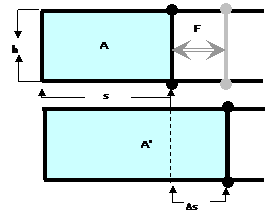

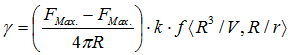 (Ring-Gleichung)
(Ring-Gleichung)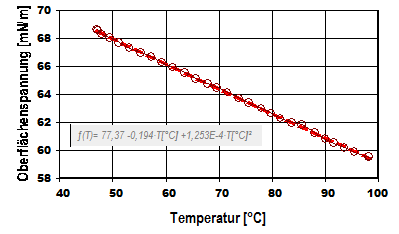

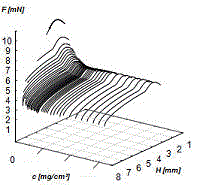
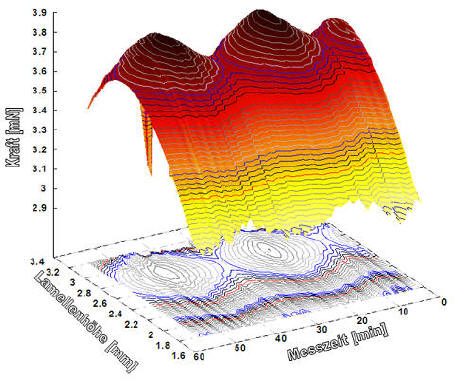

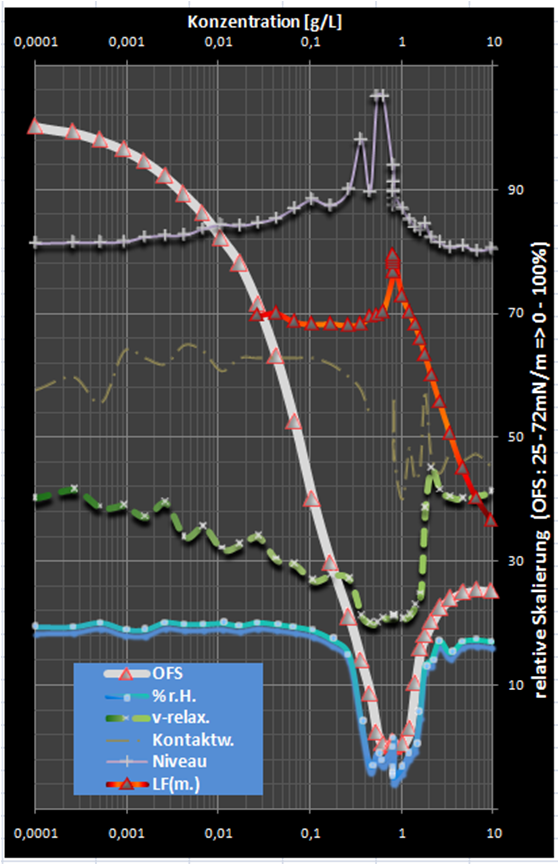



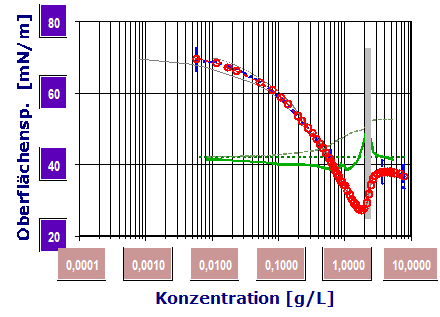
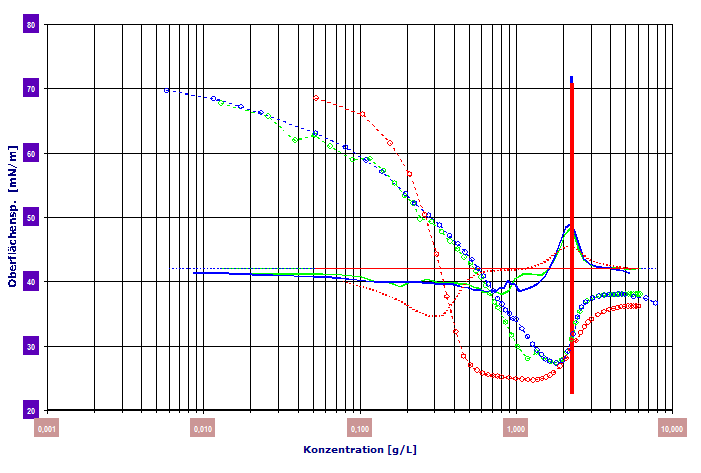

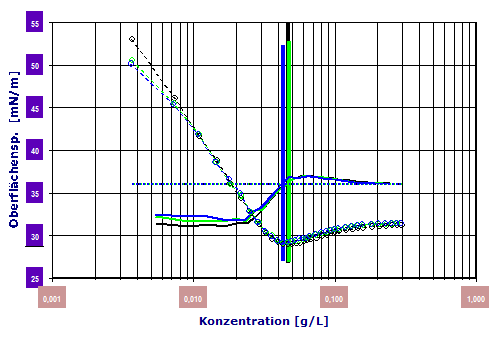
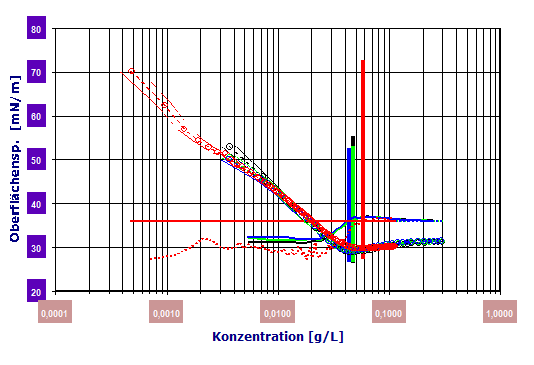
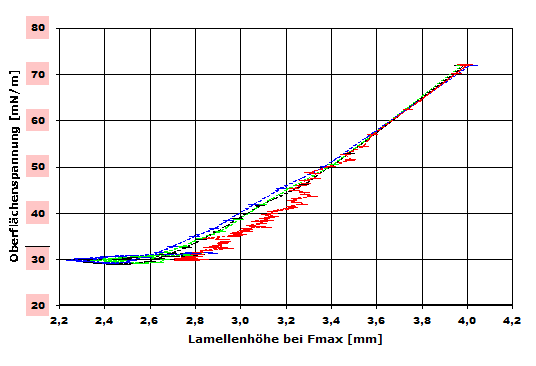
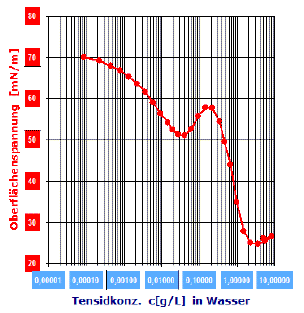

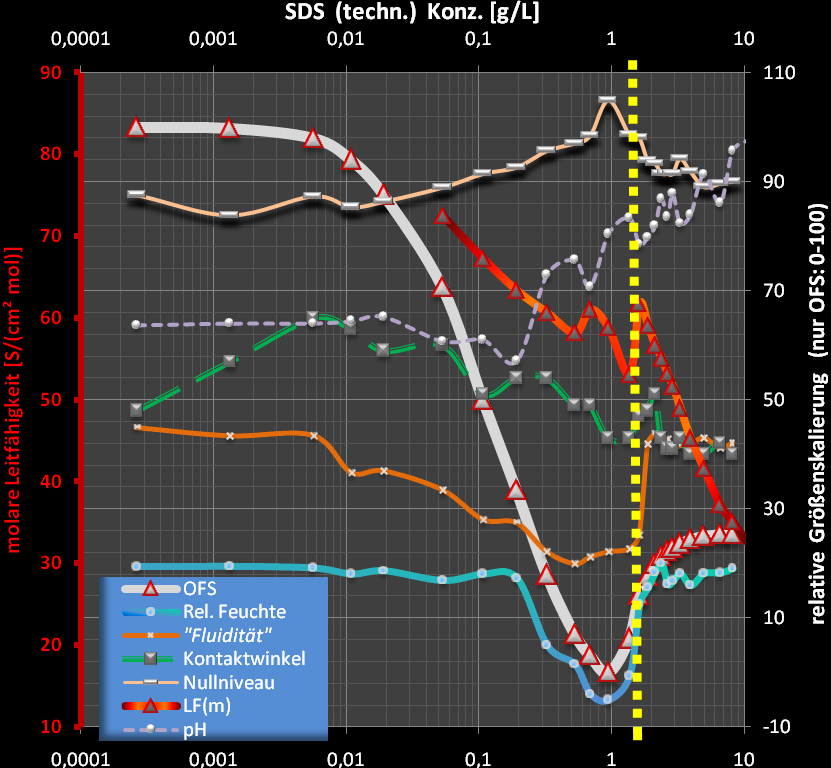
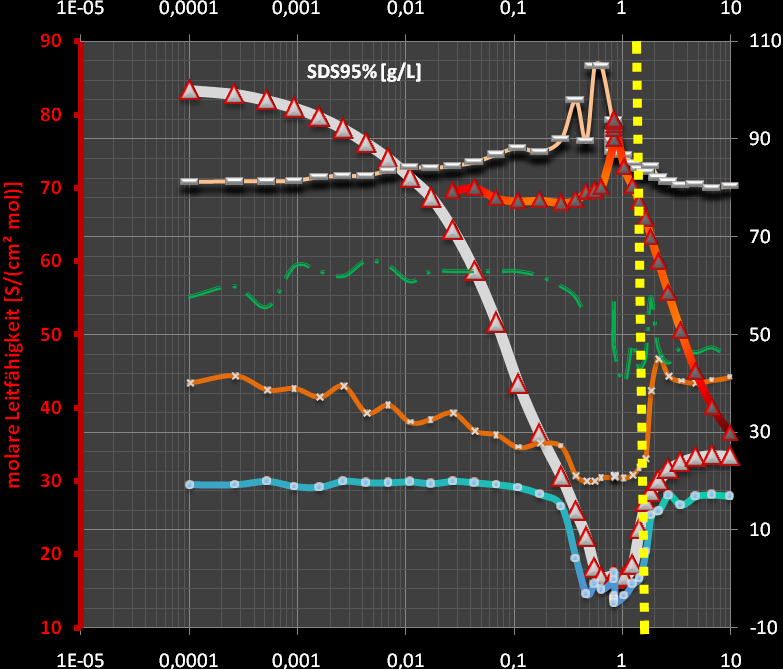
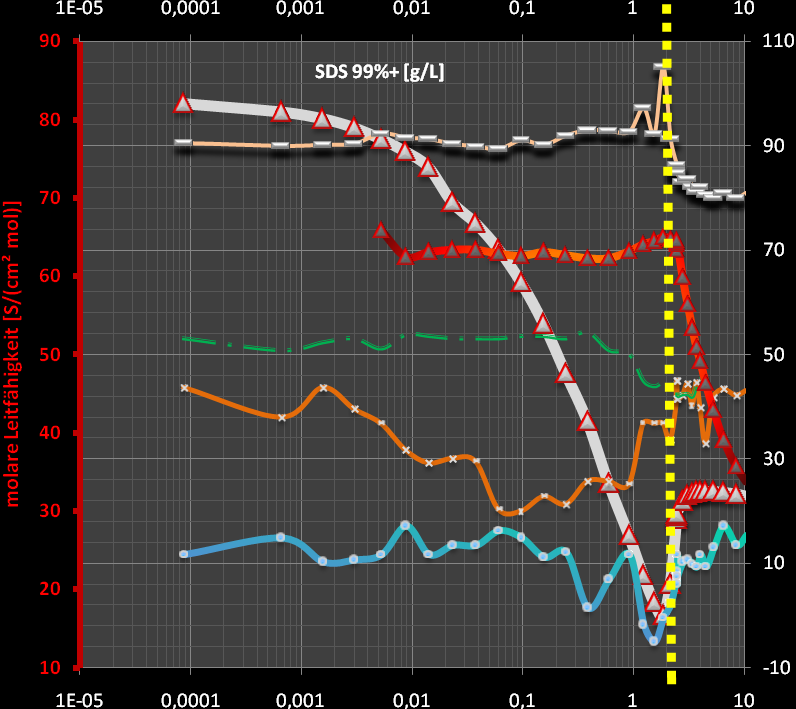
 (M=288.4g/mol)
(M=288.4g/mol)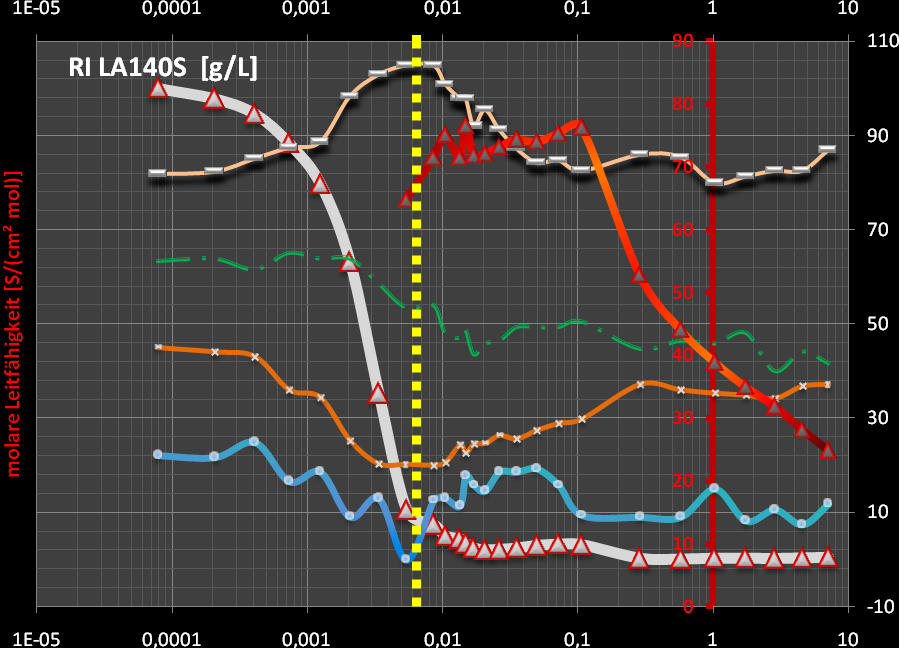
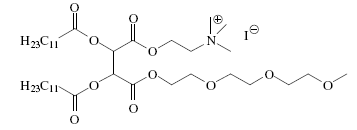
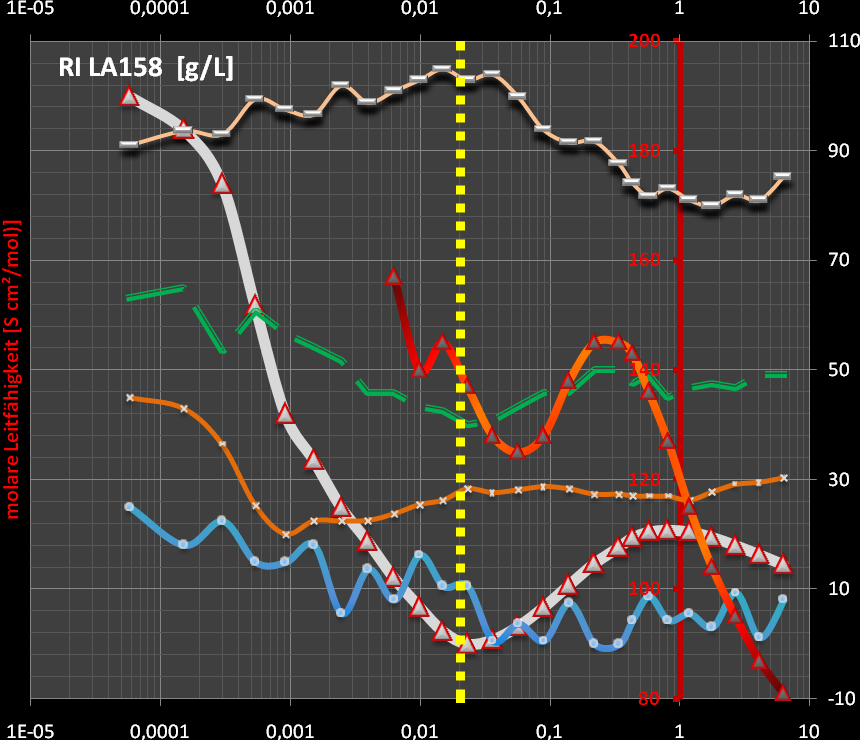
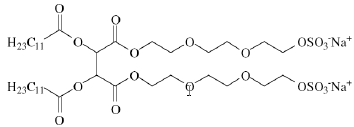


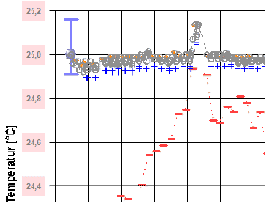




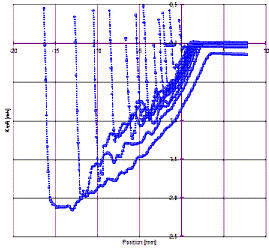
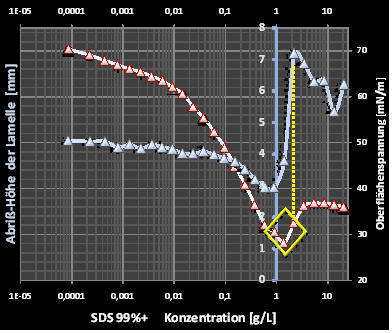 #
#