Viskositätsmessung mit axial umströmter Ringspalt-Geometrie"Translationsviskosimeter / Rheometer"
- Quellenangabe: IMETER M5/M20 von Thomas Petzoldt und Michael Breitwieser - In den unten stehenden Abbildungen ist links die Skizze eines Aufbaus der IMETER Methode M5 "DiVA", rechts die Fotographie des demgemäßen Modells abgebildet.
Funktion der Strömungsgeschwindigkeit im RingspaltDie Herleitung der IMETER-Ringspaltgleichung ist ähnlich zu der, die zum Hagen-Poiseuillesches Gesetz oder auch zu Rotationsviskosimetern zu finden ist. Wir messen jedoch lineare Kräfte und nicht Volumen oder Drehmomente, weshalb die Formulierungen dementsprechend gestaltet sind. Die Kraft (Fs) die zwischen einer Flüssigkeit und einer Zylinder-Mantelfläche (2πrh) übertragen wird, ist proportional zur Viskosität (η), der Flüssigkeit und zum Geschwindigkeitsgradient (v): Der Kraft (Fp) über dem Mantelflächenelement und auf die Stirnsseite des Zylinders bezogen entspricht dem Druckabfall (Δp):
Druckabfall und viskositätsbedingter Strömungsverlust entsprechen einander. Aktio=Reaktio. Wir messen die Kraft Fp über die Kraft, die am Zylindermesskörper angreift. Differentialgleichung für die Strömungsgeschwindigkeit als Funktion des Radius:
Die Differentialgleichung wird zweimal integriert
und liefert entsprechend zwei Integrationskonstanten (C1, C2). Diese werden aus den Randbedingungen der Geschwindigkeiten auf den beiden Grenzflächen ermittelt.
Viskosität als Funktion der KraftDas pro Zeit aufgrund der Relativbewegung des Messkörpers bewegte Volumen ist gleich dem Volumen, das durch den Ringspalt strömt. Das bestimmte Integral wird ausgerechnet, die Konstanten werden eingesetzt und nach einigen Umformungen der Gleichung ergibt sich die folgende Lösung für die Viskosität:
Mit der obigen Beziehung wird die Viskosität und der Druckabfall aus der Funktion der Strömungsgeschwindigkeit eliminiert.
Die an der Wägezelle gemessene Kraftdifferenz FW ergibt sich aus der Summe zweier Kräfte. Einerseits wirkt auf den Querschnitt des Messkörpers die durch Strömungsverlust bedingte Druckdifferenz. Andererseits wirkt auf der Mantelfläche des Messkörpers die durch Viskosität des Fluids bedingte Schubspannung. Hierbei ist zu beachten, dass ein positives Vorzeichen dieser Kraft FW entsprechend der Skizze zum Versuchsaufbau in positiver z-Richtung als aufwärts gerichtet definiert wird. Durch Einsetzen und Umformen werden letztlich die folgenden Beziehungen für die Kraftdifferenz sowie die Viskosität erhalten:
(Die IMETER-Ringspaltgleichung)
Messunsicherheit / FehlerbetrachtungAls Grundlage der physikalischen Messunsicherheitsberechung zur Einschätzung möglicher Fehler werden die entprechenden partiellen Ableitungen zu den Variablen von Messung und Messkörpern gebildet (Sensivitätskoeffizienten):
Mit den folgenden beispielhaften und realistischen Eingabewerten ... wird die Kalkulation entsprechend durchgeführt: Am Ergebnis der Beispielrechnung zur Viskosität zeigt sich, dass wesentliche Fehlerbeiträge aus der Bestimmung der Radien von Messkörper und Flüssigkeitsbehälter resultieren. Aus dem Rechenbeispiel ist erkennbar, dass bereits bei vergleichsweise grober Bestimmtheit der geometrischen Verhältnisse ab initio erhaltene Resultate recht genau sein können. KorrekturenEine der Herausragenden Eigenschaften von IMETER ist die vollständige Transparenz. Lückenlos können die Eingangsdaten Weg, Zeit, Kraft, Temperatur ... aus den Ablesungen der Sensoren, die tabelliert und in Diagrammen aufbereitet werden, untersucht werden. Die automatisch generierten Prüfberichte listen zudem auch Zwischenergebnisse auf. Dadurch, dass Rohdaten gespeichert werden, stehen diese für Neuberechnungen jederzeit, sogar noch zur Prüfung anderer Theorien, zur Verfügung. Hierzu aber unten mehr. An dieser Stelle soll zuerst noch die weitere Behandlung der Viskositätsmessung thematisiert werden. - Bei relativ geringen Strömungsgeschwindigkeiten / höherer Viskosität ist die IMETER-Ringspaltgleichung unmittelbar anwendbar und liefert bereits ziemlich korrekte Ergebnisse. Anders sieht es aus, wenn Trägheitseffekte der Strömung berücksichtigt werden müssen. Dies ist im typischen Arbeitsbereich der Standardausführung von DiVA für Fluide mit η<100 mPa·s der Fall. Dann nämlich stammt ein Teil der gemessenen Kraft aus der parallel erzeugten kinetische Energie. Die Kinetische-Energiekorrektur entspricht dem Term "½mv²" wobei für v die mittlere Strömungsgeschwindigkeit vm eingesetzt wird (vm = v0·ra²/(ra²-ri²) ) und m (die Masse) aus Dichte und Strömungsvolumen stammt. Die IMETER-Methoden M5 und M6 bestimmen simultan die Dichte der Flüssigkeit, so dass die Korrekturgrößen automatisch zur Verfügung stehen. Mit dem Quadrat der Geschwindigkeit wächst neben dem Druckverlust durch die kinetische Energie auch ein Druckverlust durch die Reibung im Einlauf des Ringspalts und zur Parallelordnung der Strömung. Entsprechend wird der Energieterm (½mvm²) mit einem Geometriefaktor zeta ζ ergänzt, so, dass die Nettokraft für die Ringspaltgleichung letztlich mit Fζ = ½ vm²·ζ·ρ·π·ri² korrigiert wird. Es konnte nicht gefunden werden, dass die Auftrennung des Terms für quadratische Strömungseinflüsse (entsprechend einem Bagley-Plot) einen Vorteil mit sich bringt. ζ erhält man aus der Messung der Scherratenabhängigkeit der Viskosität (rheologische Messung) an einer newtonschen Flüssigkeit als den Faktor, der den Graphen im Diagramm Viskosität gegen Scherrate die Viskosität zu einem konstanten Verlauf bringt (z.B. bei 0.8 mm Spaltweite und 40mm Spalthöhe wird ein ζ von ~1.2 bis 1.4 erhalten). Weitere Korrekturen betreffen die Auftriebskraft von Zylinder (Fρ) und der Suspension / Aufhängung (Fhρ) sowie auch deren Ringspalt-Reibung im Fluid (Fhη), die rekursiv in einem Iterationsschritt bestimmt wird. Der Kraftbeitrag des Meniskus an der Zylinderaufhängung kann durch die Handhabung im Ablauf in der Referenzkraft (Auftriebsmessung) eliminiert werden; die betroffene Länge der Suspension - sowohl für die Auftriebskorrektur und den Reibungsterm - kann ebenfalls das selbstlernende Verfahren per Füllstandsmessung selbst ermitteln (Einzelheiten vgl. Anleitung zu DiVA-A1). Fw = F° - Fρ - Fζ - Fhρ - Fhη - FΘ Die Reynoldszahl wird wie bei Rohrströmungen mit der charakteristischen Länge d für den Ringspalt aus dem hydrodynamischen Radius mit d = 2(ra-ri) berechnet: Re = ρ · vm · d / η KalibrierungDie Methode M5 DiVA verwendet keine Kalibrierfaktoren. Die Kalibrierung erfolgt durch Messung von Standardfluiden (Wasser, Newtonschen Normalproben der Viskosität). Eine bei der Messung von Kalibrier- oder Normalfluiden festgestellte Abweichung wird durch Auslegung der Messtoleranz der Messkörpergeometrie behoben. Es handelt sich dabei typisch um einige µm oder Bruchteile davon. Insofern kann, wenn exakte Messkörper zur Verfügung stehen, die Viskosität über angeschlossene Normale von Zeit/Länge und Kraft (Masse) metrologisch absolut dargestellt werden. Für praktisch relevante Genauigkeitsanforderungen können - abgesehen vom Innendurchmesser der Röhre - die Proportionen der Teile von DiVA innerhalb des IMETER-MessSystems durch Mittel und Methoden, die das System selbst enthält, bestimmt werden. Im Einzelnen dienen als Bordmittel hierzu das eingebaute E2 Justiergewicht der Wägezelle für die Massebestimmung. Die geometrischen Abmaße sind über den Vergleich mit Normal-Endmaßen zusammen mit der Plattformsteuerung möglich; Dichte, Volumen und Ausdehnungskoeffizient sind über die fehlerfreie Dichtemessung exakt messbar (→ IMETER-Dichtemessung). Das IMETER MessSystem ist damit ein autarkes und autonomes Viskositätsmessgerät.
Wie aus Kraftmessungen z.B. die Temperaturabhängigkeit der Viskosität erhalten wirdIMETER speichert bei Messungen auch die Rohdaten. Damit können frühere Messungen mit künftigen Theorien oder nachkorrigierten Messkörperdaten stets neu berechnet werden. Woran nicht zu deuteln ist, ist a priori die Beobachtung, d.h. die Ablesung der Sensordaten. Während bei Geräten anderer Hersteller und Messprinzipien Rohdaten von eher kryptischer oder zumindest partiell willkürlicher Natur sind (Drehmomente, Drücke, Durchlaufzeiten), stammen die IMETER Rohdaten aus geordneten Zusammenhängen mit separat kalibrierbaren Datenquellen. - Wie hier aus Kraft und Geschwindigkeit in der geometrischen Anordnung die Flüssigeigenschaft hervorgeht, dazu im Folgenden Dokumente aus einer Messung. |
| Das Diagramm rechts (Abb.3) zeigt die Rohdaten eines Viskositätsmesswertes. Gegen die X-Achse, die die Position der Zylinderunterkante in der Röhre anzeigt, ist die gemessene Kraft angetragen. (Das Diagramm ist der Rohdatenansicht der automatischen Dokumentation entnommen; hier werden Positionen oberhalb des Bezugspunktes <Boden der Röhre> negativ angezeigt, weil die Plattform zur Messung der Zugkraft nach unten läuft). Aus der Ruhelage bei -5mm wird der Messkörper mit konstanter Geschwindigkeit gezogen. Weil Kraftwerte aus der Wägezelle bereits vor dem Beginn der Bewegung aufgezeichnet werden, wird die Ausgangskraft miterfaßt. Mit der Bewegung steigt die Kraft steil an und erreicht einen stationären Wert. Die stationäre Kraft (F°) hier bei 561 mN, bedarf, wie beschrieben, einiger Korrekturen bevor sie als Eingangswert Fw für die Ringspaltformel verwendet werden kann. |
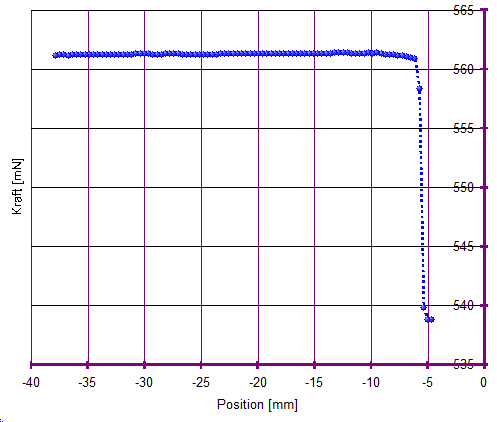 Abb.3 - ein Viskositätsmesswert Abb.3 - ein Viskositätsmesswert |
|
Abb. 4 zeigt vergrößert die Einzelwerte der stationären Kraft von der Messkurve in Abb.3. Die so erkennbare Schiefe und Rauigkeit des Verlaufs bilden per Mittelwert und Standardabweichung einen Beitrag in der Berechnung der Messunsicherheit - zusätzlich zu den geometriebedingten Messunsicherheiten und der Messunsicherheit von Temperatur, Masse und Fallbeschleunigung. Die Rauigkeit der Kurve - das sind Druckschwankungen - wird zu Noise quantifiziert und berechnet: Noise wird erhalten, indem für jedes Kraftwertepaar |ΔY|/ΔX summiert wird (numerisch integriert). Der Mittelwert davon in der Einheit µN/mm wird ausgegeben. |
Abb.4 - Der Messwert gezoomt. Die Schiefe und Streuung liefert einen Beitrag in der Berechnung der individuellen Messunsicherheit des Viskositätsmesswertes. |
| Rheologische Messungen zeigen bisweilen bei bestimmten Scherraten bemerkenswerte Maxima (z.B. Buttermilch mit 'Butterflocken').
Die Daten stammen aus einer Messung an einem Motoröl. Dabei wurde die Temperatur stufig von 100, 80, 60 nach 40°C geändert. Daher stammen die Messkurven der Abb. 3 bis 5. In Abb.5 sind alle 36 Messkurven übereinander gelegt. Die neun je Temperaturniveau zusammenfallenden Kraft-Weg-Kurven zeigen sich untereinander als deckungsgleich reproduzierbar. Die Lageunterschiede der stationären Kräfte im Temperaturabstand von 20 K (keine Zeiteffekte) sind praktisch nicht ununterscheidbar. Den Bericht zu dieser Messung finden Sie als PDF hier: Motoröl_100-40°C.pdf |
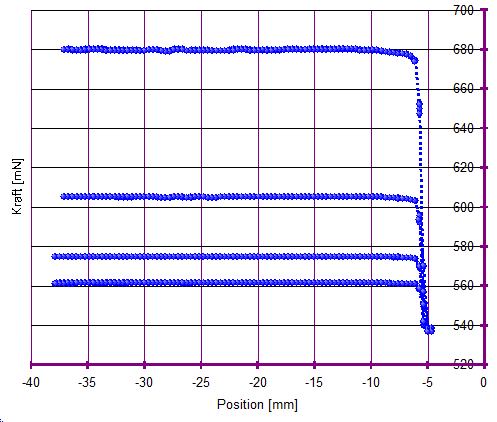 Abb.5 - Messung der Temperaturabhängigkeit (36 Messwerte) Abb.5 - Messung der Temperaturabhängigkeit (36 Messwerte) |
| Die Auswertung unter Berücksichtigung der Temperaturabhängigkeit der Körper und Dimensionen erlaubt die Berechnung der Viskosität zur jeweiligen stationären Kraft.
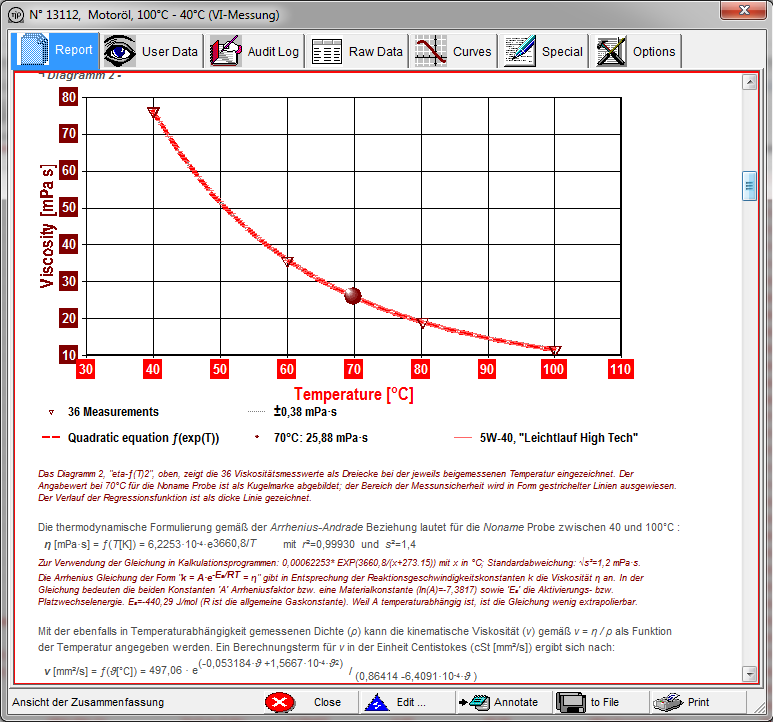
Abb. 6 zeigt die erhaltenen 36 Viskositätswerte als Dreiecke und mit einer geeigneten Regressionsfunktion gefittet (rote Linie). So können dazwischen liegende Viskositätswerte über die Funktionsgleichung interpoliert werden.
|
Abb.6 - Temperaturabhängigkeit der 36 Messwerte. |
|
Für viele Maßzahlen zur Charakterisierung flüssiger Materie ist IMETER ein System, dass die Breite von Umgebungs- und Prozessvariablen bedient. Das IMETER-Framework bietet auf einfache und unprätentiöse Weise alles, um Abläufe und Messungen zu steuern, Daten zu sichern, zu sichten, zu verifizieren, auszuwerten, zu exportieren und zu vergleichen. Wahrscheinlich ist das IMETER Framework das komplexeste, kompletteste und einfachste Werkzeug, das Ihnen bei Messgeräten begegnen kann. Die Abbildungen unten zeigen an dem vorgestellten Beispiel, wie die relevanten Daten zur Viskosität dargestellt und inspiziert werden können. |
|
|
Es wird die Reportansicht gezeigt, in der ein Ausschnitt der tabellarischen Daten gezeigt wird. Neben den kennzeichnenden Angaben in der ersten Tabelle finden sich in den beiden anderen Listen auch die berechneten Korrekturen, die Fehlerangabe und Messkörperdimensionen (vgl.: Motoröl_100-40°C.pdf). |
|
|
Das Forscherbedürfnis, Tabellen und Daten der Diagramme leicht in andere Datenverarbeitungsprogramme übertragen zu können, ist vielfach berücksichtigt. |
Abb.8 - Der Report - Mit Grafiken, Tabellen und Erklärungen.
|
|
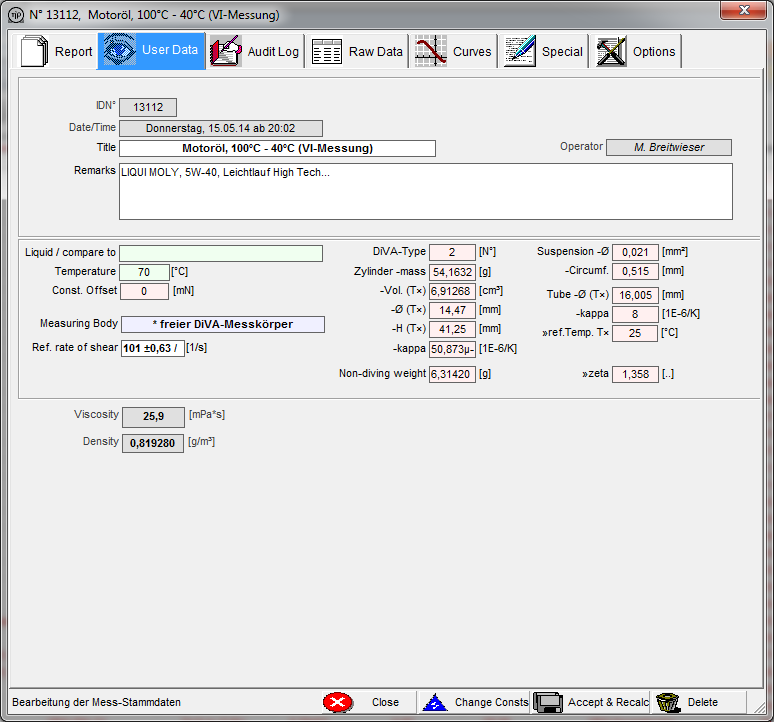
In Abb.9 wird ein das Register des Datenfiles angezeigt, das die Angaben des Anwenders und die Daten des Messkörpers zeigt. Normalerweise werden die Messkörperdaten nicht explizit angegeben, man kann sie aber bearbeitbar schalten, verändern und sehen, welches Ergebnis sich dann ergibt (mit Audit-Log werden solche Spielchen für eine evtl. Zurücknahme registriert).
|
Abb.9 - Die Angabedaten - Messkörperdaten. |
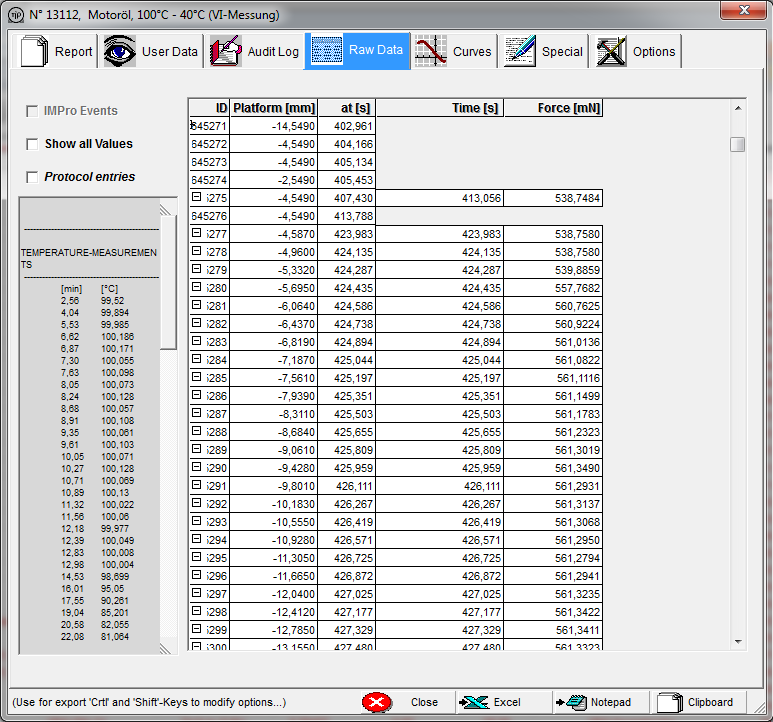
| Abb. 10 präsentiert die Rohdaten als Tabelle im Key-Value-Format. Jeder Kraftmesswert hat einen Indexwert, einen Zeitpunkt und eine Position. Auf diesen Grunddaten beruhen zusammen mit den Messkörperdaten die Berechnungen. Die geordneten Daten können mit der Befehlsschaltfläche bequem z.B. nach Excel kopiert werden. |
x
Abb.10 - Die Rohdaten (Weg, Zeit, Kraft, Temperatur). |
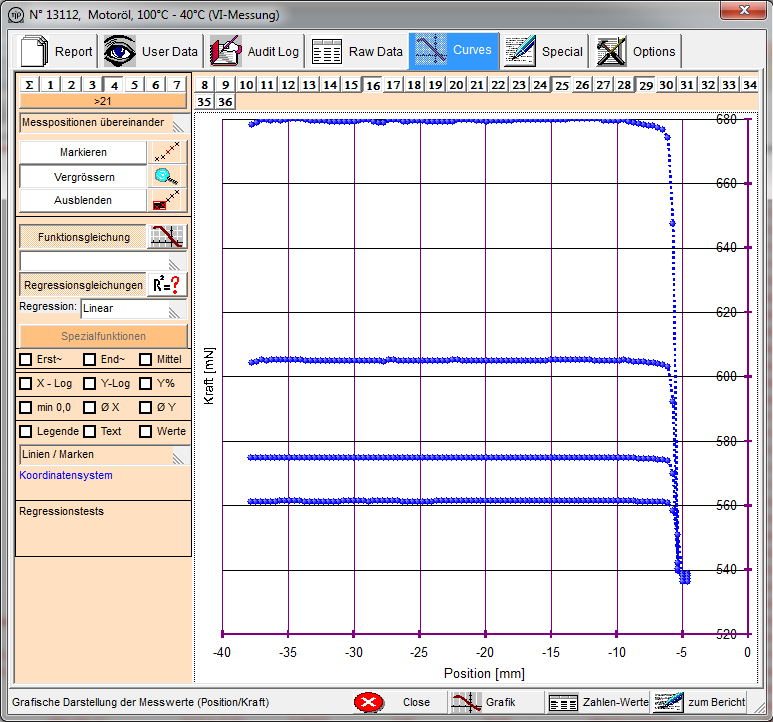
| Im nächsten Tab, Abb. 11, befindet sich die grafische Aufbereitung der Rohmessdaten. Hier können die Daten auf einfache Art in einen "selbst-verständlichen" physikalischen Zusammenhang gebracht werden.
|
x
Abb.11 - Die graphische Aufbereitung der Rohdaten. |
ViskoelastizitätDie Viskoelastizität ist bei nieder- bis mittelviskosen Fluiden eigentlich kein Thema. Sie kann gleichwohl Gegenstand einer weiteren Auswertung werden. Sowohl die Retardation als auch Relaxation ist durch entsprechende Verfahrensmöglichkeiten darstellbar. Daten zur Messung des Abklingens der Kraft nach (sprunghafter) Dehung sind unmittelbar und einfach zugänglich (Spannungsrelaxation). Die zeitliche Veränderung unter konstanter Spannung (Retardation, Kriechversuch) und Oszillationsmessungen (axiale Sinusschwingung der Röhre) bedürften für letztgenannte jedoch eine Erweiterung der Steuerungstechnik im IMETER-Framework - oder es würden dazu lineare Beschleunigungen angewendet. Scheinbare ViskositätDie Viskosität kann nur für Newtonsche Fluide angegeben werden. Warum? Was bedeutet das? -- Die Herleitung jeglicher Viskositätsmessung geht von einem parabelfömigen Strömungsprofil aus. Auf dieser Grundlage ist die Viskosität einer Flüssigkeit eine Eigenschaft, die für alle Röhrendurchmesser und Pumpgeschwindigkeiten zu kalkulierbaren Ergebnissen führt. Strömungen von Fluiden, die einen nicht-paraboloides Profil aufweisen, sind nicht-newtonisch und wegen dieser fehlenden Grundvoraussetzung nicht entsprechend kalkulierbar. Rechungen und Vorhersagemöglichkeiten gelten bei diesen genau genommen nur für die jeweiligen Spaltweiten bzw. Röhrendurchmesser, Wandungseigenschaften und Schergeschwindigkeiten. Daher werden auch Messgeräte je nach Konfiguration entsprechend unterschiedliche Ergebnisse anzeigen. Zu den Abweichungen der Strömungsprofile und entsprechender formelmäßiger Begleitung (zahlreiche Modelle existiern), kann gleichwohl auch bei einer nicht-Newtonschen Viskositätskurve die jeweilige Schergeschwindigkeit ein parabelförmiges Strömungsprofil haben. - Wir wollen diese Thematik bei Gelegenheit IMETER-Messtechnisch erörtern. Das IMETER Modul M5 "DiVA" berechnet, wie eben ausführlich beschrieben, schlicht die Viskosität. Ob es sich um eine scheinbare Viskosität handelt, kann bei einer einzelnen Messung mitunter am Verlauf der quasistationären Kraft und bei rheologischen Messungen daran erkannt werden, dass im Viskositätsdiagramm kein konstanter Viskositätswert für die verschiedenen Schergeschwindigkeiten ausgegeben wird (die Auswertungsoftware schaltet dann auch automatisch von der Betitelung 'Viskosität' zu 'scheinbare Viskosität' um); so kann Strukturviskosität am Abfallen der Vikositätskurve und Dilatanz am Anstieg derselben erkannt werden. |
|

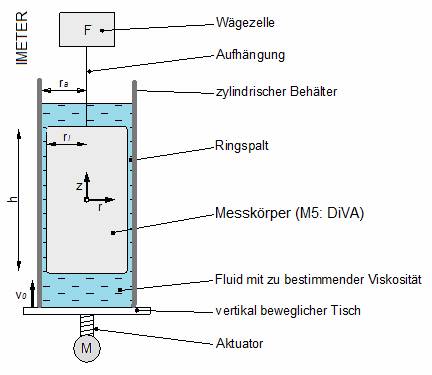


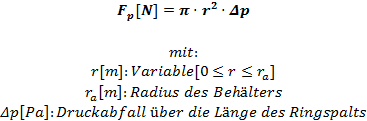
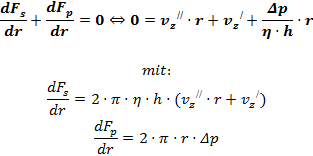
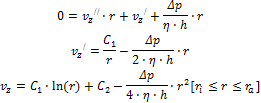
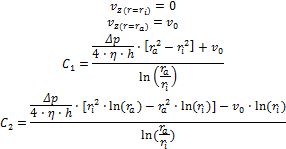
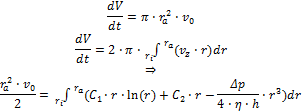
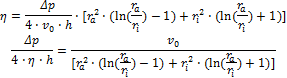
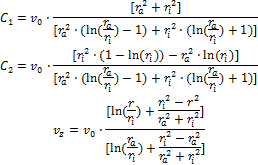
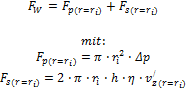
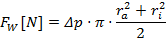

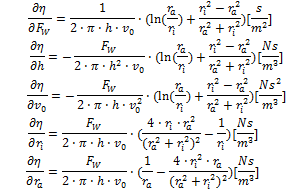
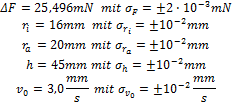
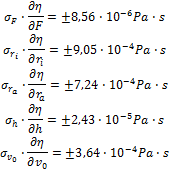
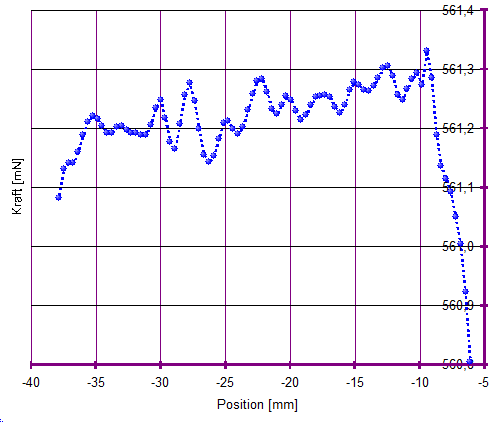
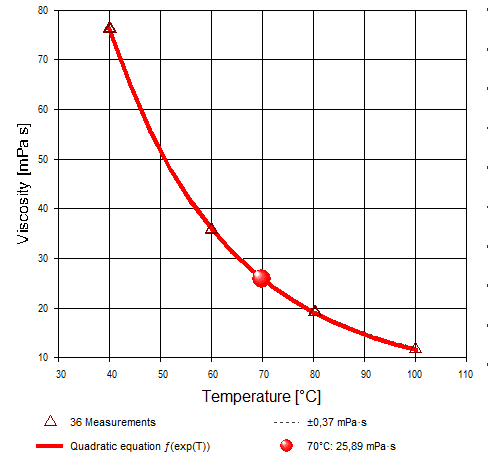
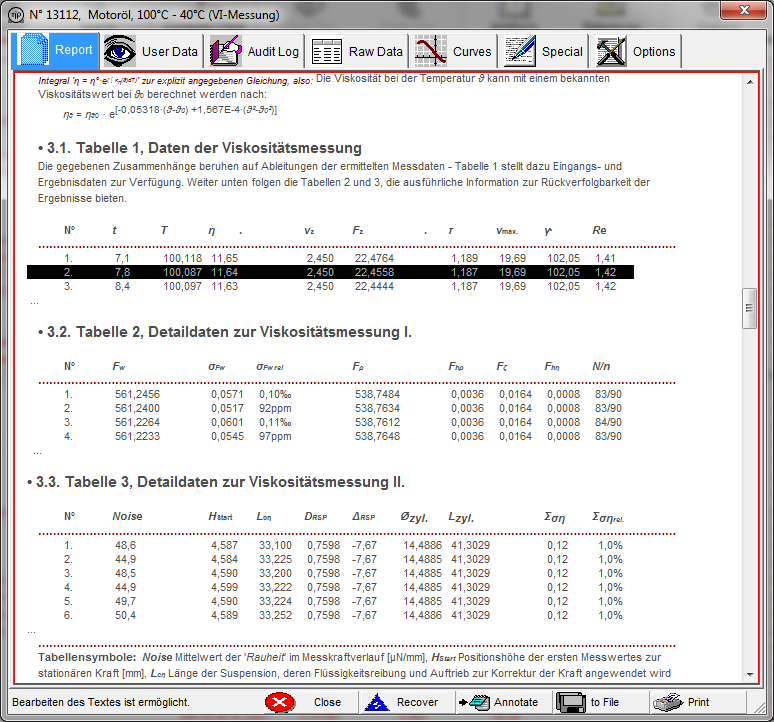 Abb.7 - Tabellenausschnitte zur Viskosität.
Abb.7 - Tabellenausschnitte zur Viskosität.