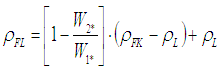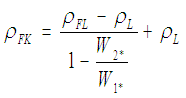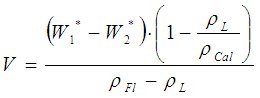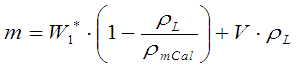DichteBegriffe, Geräte, Messung und Berechnung
Sie finden auf dieser Seite Beiträge zum Themenkreis "Dichte" - Definitionen,
 hydrostatischen Flüssigkeits-Dichtemessung durch die Bestimmung des Auftriebs einer exakten Kugel in einer thermostatisierten Messzelle (IMETER M8)Zusammenhänge, Einflüsse und Beschreibungen der Messmethoden teilweise unter Angaben einschlägiger Normen. Auf dieser Seite versuchen wir alles Wesentliche in Zusammenhang mit der Messung der Dichte aktuell darzustellen. Sie können uns dabei helfen und auf Korrekturen oder Fehlendes aufmerksam machen. hydrostatischen Flüssigkeits-Dichtemessung durch die Bestimmung des Auftriebs einer exakten Kugel in einer thermostatisierten Messzelle (IMETER M8)Zusammenhänge, Einflüsse und Beschreibungen der Messmethoden teilweise unter Angaben einschlägiger Normen. Auf dieser Seite versuchen wir alles Wesentliche in Zusammenhang mit der Messung der Dichte aktuell darzustellen. Sie können uns dabei helfen und auf Korrekturen oder Fehlendes aufmerksam machen.
1. DichteDie Dichte (Massedichte, spezifische Masse, density), Formelzeichen ρ (rho), ist der Quotient aus Masse m und Volumen V (ρ=m/V), d.h. "Masse pro Volumen". Die Dichte ist der Zahlenwert der Massenkonzentration. Die gesetzliche Einheit ist kg/m3, gebräuchlich ist auch g/cm3. Der Kehrwert der Dichte 1/ρ heißt spezifisches Volumen (specific volume). Früher verwendete und verwandte Bezeichnungen im Zusammenhang mit der Dichte sind: Dichtigkeit, Wichte, Artgewicht und spezifisches Gewicht. Die Wichte, Formelzeichen γ (gamma), ist der Quotient aus der Gewichtskraft G und dem Volumen V eines Körpers bzw. einer Stoffmenge (γ = G/V). Die Wichte lässt sich darstellen als Produkt aus der Dichte ρ eines Körpers und der lokalen Fallbeschleunigung g, also: γ = ρ·g. Unter den Synonymen ρn Dichtezahl, relative Dichte versteht man das Verhältnis der Masse eines Körpers zur Masse einer volumengleichen Menge einer Standardsubstanz ρ0. Standardsubstanz ist zumeist Wasser bei 4°C oder auch Quecksilber (ρn=ρ/ρ0). Durch diese lokal realisierbaren Standardbezüge wird das Problem von der Ortsabhängigkeit der Fallbeschleunigung (Schwerkraft) umgangen, außerdem ist der dimensionslose Zahlenwert auch in allen nichtmetrischen Einheiten der Welt vergleichbar (specific gravity). Einheit von Wichte und spezifischem Gewicht war p/cm3 (p=Pond). Falls die Fallbeschleunigung der Normal-Fallbeschleunigung entspricht, sind Werte für Wichte in p/cm³ und Dichte in g/cm³ zahlengleich. Zu erwähnen ist, dass spezifisches Gewicht heute noch oft als äquivalenter Ausdruck für Dichte gebraucht wird. Die Dichte ist druck- und temperaturabhängig. Die Temperaturabhängigkeit wird durch den Ausdehnungskoeffizienten, die Druckabhängigkeit durch die Kompressibilität bzw. bei Feststoffen durch das Kompressionsmodul ausgedrückt. Eine präzise Dichteangabe, insbesondere für fluide Stoffe, umfasst unbedingt die Nennung der zugehörigen Temperatur. Die Druckabhängigkeit der Dichte im Schwankungsbereich des Normaldruckes ist – außer bei Gasen – unbedeutend.
|
2. AusdehnungskoeffizientMit zunehmender Temperatur vergrößert sich das Volumen von festen, flüssigen und gasförmigen Stoffen, d.h. die Dichte der Stoffe nimmt mit steigender Temperatur ab. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
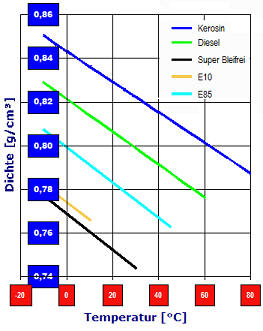
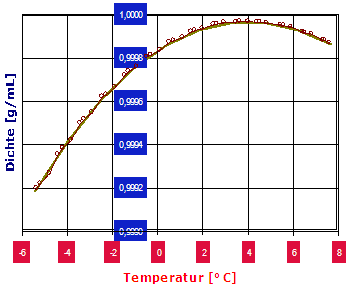
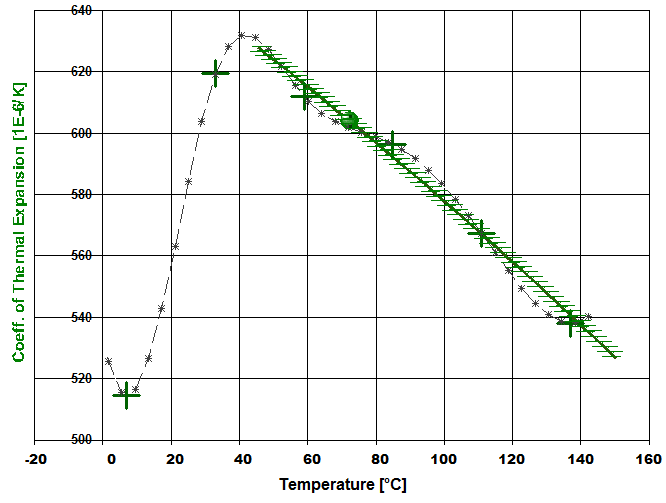
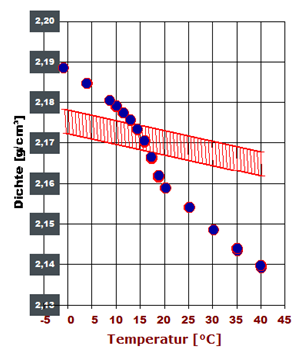
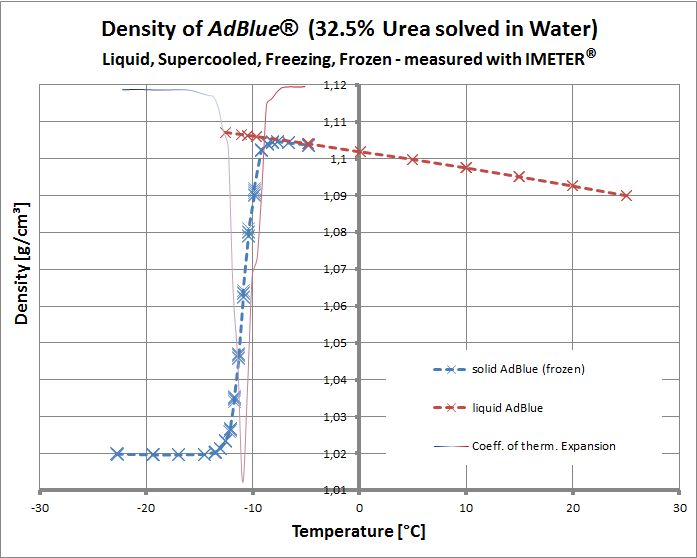
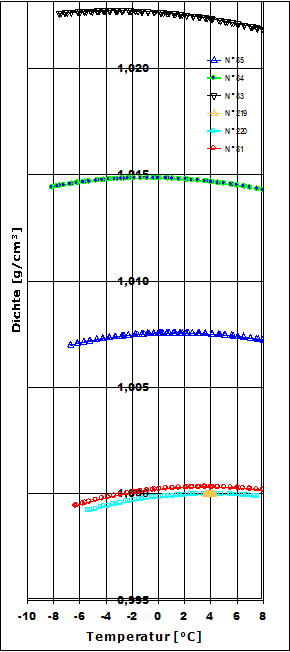
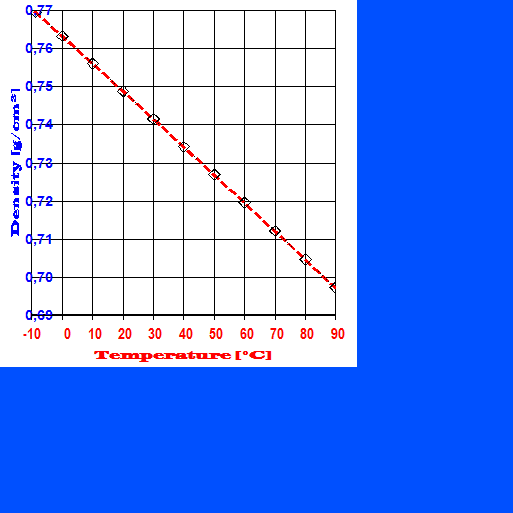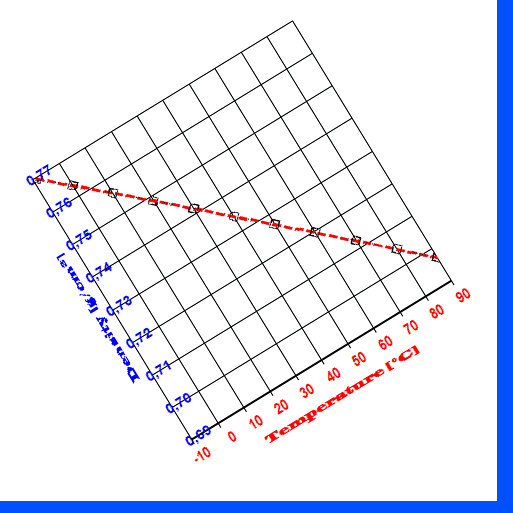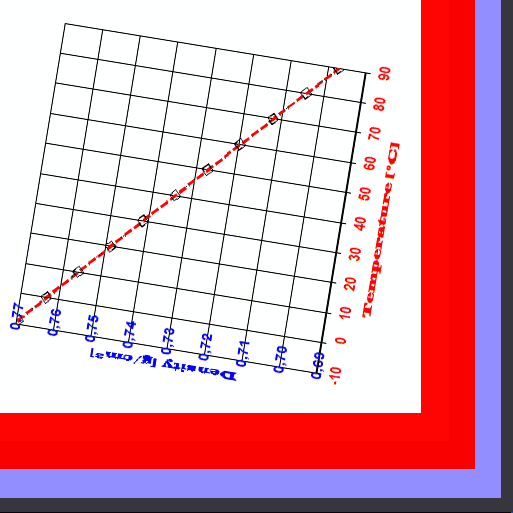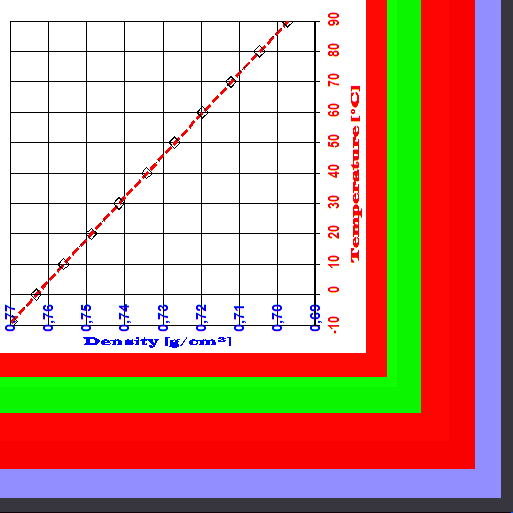
In Abb.1 ist am Beispiel von Kraftstoffen die deutliche Abhängigkeit der Dichte von der Temperatur zu erkennen. Vom Normalfall, also der ziemlich linearen Dichteabnahme mit der Temperatur, gibt es Ausnahmen. Zu diesen zählen: Wasser zwischen dem Gefrierpunkt und 4°C (Anomalie des Wassers [Abb. 2, rechts]), spezielle Glaskeramiken (z.B. Zerodur®), β-Quarz, β-Eukrypt, gewisse Kohlefasermaterialien sowie sphärische Körper spezieller Morphologie (►dokumentierter Sonderfall). Ursache der thermischen Materieausdehnung ist der zunehmende Raumbedarf der Teilchen bei steigender Temperatur. In physikalischer Formulierung ist der Raumausdehungskoeffizient κ: κ = 1/V· dV/dT Der Wert von κ (kappa) kann für grobe Berechnungen über ein gewisses Temperaturintervall als genügend konstant angenommen werden. Teflon (PTFE) bei 19°C ist bezüglich der Linearität eine klassische Ausnahme (vgl. Abb.6 weiter unten). Der Koeffizient κ heißt korrekt kubischer thermischer isobarer Ausdehnungskoeffizient. Verkürzt spricht man vom kubischen Ausdehnungskoeffizienten oder auch vom Raumausdehnungskoeffizienten. Während üblicherweise κ für Fluide angegeben wird, findet sich für Feststoffe normalerweise der lineare thermische isobare Ausdehnungskoeffizient (α, alpha). Die gebräuchliche Einheit für α ist 10-6K-1. Dazu ist der äquivalente Ausdruck "µm·m-1·K-1 ", der bedeutet, dass Temperaturänderungen von einem Grad Längenänderung von α Mikrometern an einem 1 Meter langen Stab bewirken. Für Flüssigkeiten ist die Wärmedehnung deutlich größer, und der Wert wird als Raumausdehnungskoeffizient κ in vielfachen von 10-5K-1 angegeben. Der Koeffizient der thermischen Längenänderung (α) wird in Modellrechnungen oft als raumrichtungs-, temperatur- und druckunabhängig angesehen. α kann bei Stoffen, die aus geordneten Strukturen aufgebaut sind, jedoch Raumrichtungsabhängig (anisotrop) sein, wie übrigens auch die Wärmeleitfähigkeit.Bei Kochsalz (NaCl) ist α in allen drei Raumrichtungen gleich und beträgt αx = αy = αz = 40 µm·m-1·K-1. Bei Calzit (CaCO3) hingegen, ist α in zwei Raumrichtungen negativ αx = αy = -6 µm·m‑1·K‑1 und in der dritten positiv, αz = 26 µm·m‑1·K-1, so dass ein Ausdehnungsplus überwiegt. Bei β-Eukrypt (LiAlSiO4) mit αx = αy =7.8 und αz = -17.8 µm·m-1·K‑1, d.h. es überwiegt die negative Ausdehnung; bei Aragonit (chemisch ebenfalls CaCO3) ist α in allen drei Raumrichtungen verschieden: αx =10, αy = 16, αz = 33 µm·m-1·K-1. Der lineare Ausdehnungskoeffizient α kann darum für Feststoffe nicht sicher aus α = κ / 3 angegeben werden. Da (Teil-)Kristalline, nicht-amorphe, gereckte oder verstreckte Materialien längs einer Orientierung oft verschiedene α haben (αx, αy, αz) als quer zu ihr. Bei Feststoffen ist "κ =3α", wie an den Beispielen gezeigt, zumindest riskant. Die in den Tabellen rechts aufgelisteten Einträge geben eine Übersicht zur Unterschiedlichkeit dieser Koeffizienten für feste und flüssige Stoffe. Der Wert von κ ist für Festkörper, wenn man von Kunststoffen absieht, grob eine Größenordnung kleiner und für Gase etwa 3 bis 10 x größer als bei Flüssigkeiten.
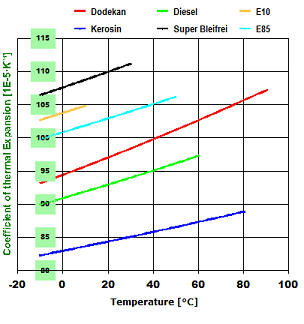
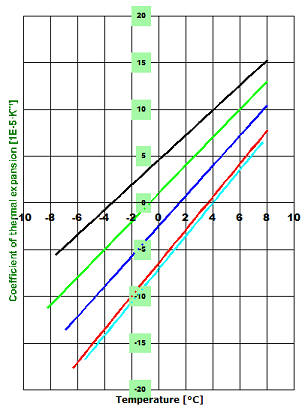
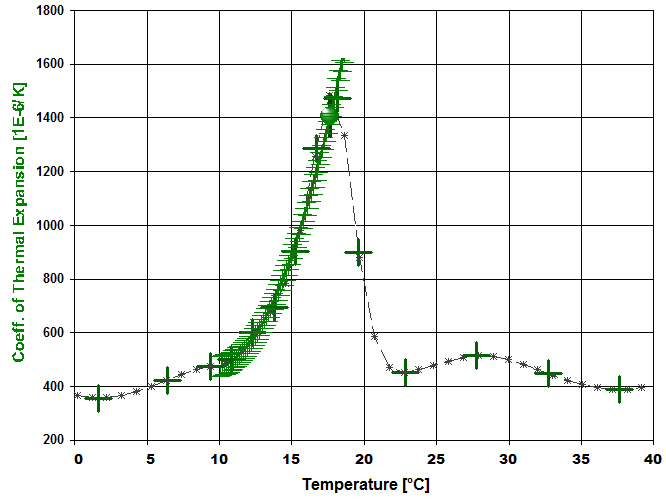
Abb.4: Temperaturabhängigkeit der Ausdehnungskoeffizienten der verschiedenen Kraftstoffe (vgl. Diagramm Abb.1 oben entsprechende Dichteverläufe) und n-Dodekan als Vergleich. |
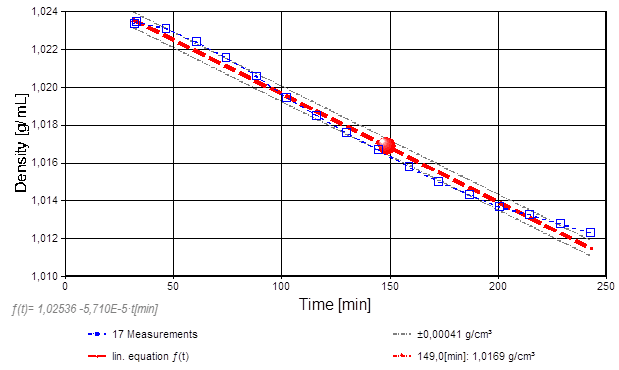
Abb.2: Dichtemessung von reinem Wasser zwischen -5 und 8°C. Das Dichtemaximum liegt bei 4°C (Wasser von 1° und 8°C ist von gleicher Dichte, es kann, da gleichdicht, quasi nebeneinander vorliegen).
Flüssigkeitsdichtetabelle unten: Die Angaben in den Tabellen stammen aus verschiedenen Quellen und sind ohne Gewähr. (Dichtedaten großteils aus [Lit.12], Mit * sind Messungen von IMETER an individuellen Proben gekennzeichnet; PDF-Doku als Link.)
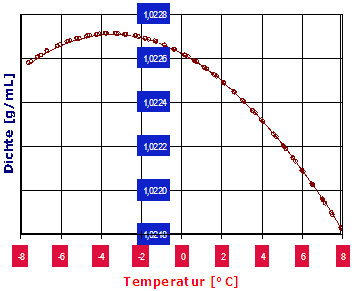
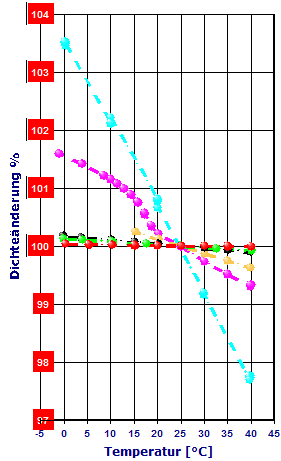
Abb.5: Wasser/Salzwasser - Ausdehnungskoeffizienten in Temperaturabhängigkeit - aus Dichtemessungen an Wasser mit 3%, 2% und 1% Kochsalz, Leitungswasser (aus Augsburg) und reines Wasser. Der Nulldurchgang gibt die Temperatur des jeweiligen Dichtemaximums an (d.i. der Parabelscheitel im Dichte-Temperaturverlauf => Abb.2 und Abb.3).
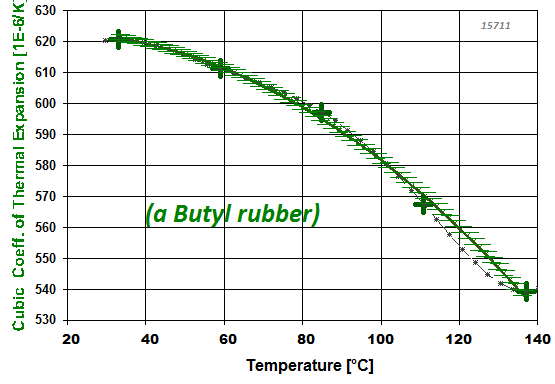
Abb.5a: Temperaturabhängigkeit des kubischen Ausdehnungskoeffizienten bei (einem) Bytylkauschuk: Der große Wert ist für weiche Kunststoffe typisch, Die Abnahme im Temperaturverlauf kann der zunehmenden Härte (Gummieleastizität) zugeschrieben werden. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Sich drehende Bimetallspiralen (Bimetallthermometer), abblätternde Beschichtungen und wandernde Klebefolie auf Glasscheiben, Verwitterung und Rißbildung werden durch Temperaturwechsel bei Verschiedenheit von κ in Materialverbünden hervorgerufen bzw. begünstigt. Für Gläser ist mit dem Wert κ die Temperaturwechselbeständigkeit verknüpft und zwar derart, dass je kleiner κ ist, die Abschreckbarkeit verbessert wird. Z.B. hat ein Geräteglas 20 mit κ= 4,5 eine Temperaturwechselbeständigkeit von 190 K; Pyrex-Glas hingegen erreicht mit κ= 3,2 immerhin schon 250 K. Und Quarz, κ= 0,5, kann glühend in Wasser abgeschreckt werden. In sogenannten Lavalampen ist der Effekt verschiedener Ausdehnungskoeffizienten (von zwei nicht-mischbaren Flüssigkeiten ähnlicher Dichten) sehr anschaulich. Durch die Lampe wird die Flüssigkeit von unten beleuchtet und erwärmt. Die etwas dichtere und zumeist gefärbte untere Phase hat einen größeren Ausdehnungskoeffizienten und wird im temperaturbedingten Konvektionsstrom/Dichtegradient in Blasen nach oben gedrückt, wo sie fern von der Heizquelle abkühlt und niedersinkt. Meeresströmungen, Wind, Wetter, auch Plattentektonik und Vulkanismus stellen Konvektionsströmungen dar, deren Ursache Dichteunterschiede in den Stoffmengen sind. Die thermische Ausdehnung verwandelt im Schwerefeld Temperaturunterschiede in Bewegung. Dort, wo Dichteunterschiede keine Konvektion mehr verursachen, funktioniert so manches nicht mehr; es ist nicht möglich ohne Gravitation eine Kerze brennen zu lassen.
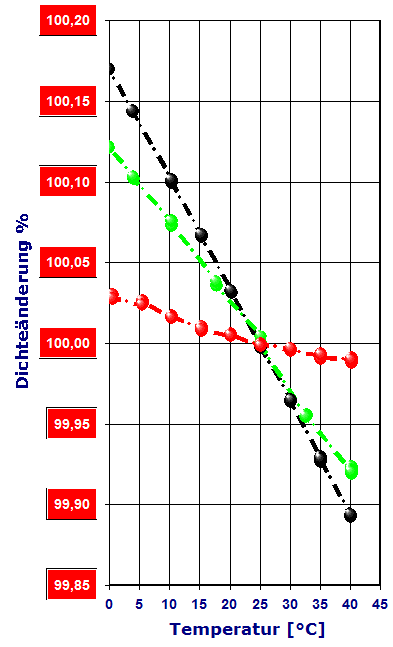
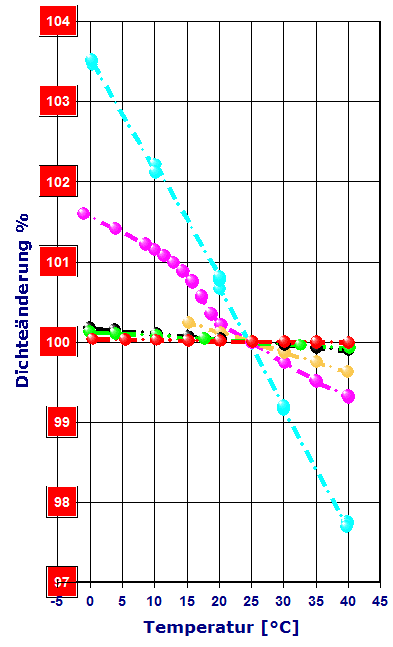
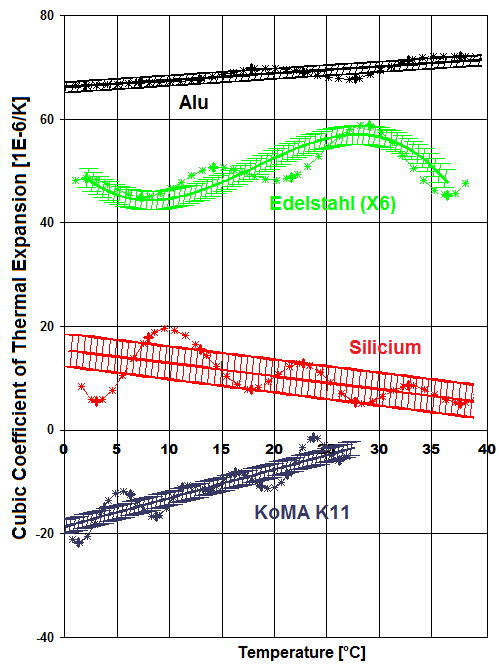
Abb.6: relative Änderung der Dichte mit der Temperatur, Bezug ist 25°C: Vergleich der Thermodilatation, verschiedener Materialien. ►rot =Silizium (10), ►grün =Edelstahl (50), ►schwarz =Aluminium (70); ►ocker =Plexiglas (PMMA) (250), ►violettrosa= Teflon (PTFE) (350 - 1500), ►türkis =Vaseline (1500) In Klammern ist der kubische Ausdehnungskoeffizient [10-6K-1] angegeben. |
Feststoffdichtetabelle: Die Angaben in den Tabellen stammen aus verschiedenen Quellen und sind ohne Gewähr. Insbesondere die Widersprüchlichkeit der Werte für κ bzw. α in der Literatur ist anzumerken. Mit * sind Messungen von IMETER an individuellen Materialproben gekennzeichnet; PDF-Doku als Link.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. Kompressibilität, KompressionsmodulDie Kompressibilität (Χ) von Flüssigkeiten drückt deren Volumenelastizität aus. Die Volumenänderung (dV) eines gegebenen Volumens (V) wird durch eine Druckänderung (dV) bewirkt: dV = -Χ·dp·V. Der Proportionalitätsfaktor ist Χ (Chi). Die Kompressibilität von Flüssigkeiten ist gering, sodass Flüssigkeiten oft als inkompressibel angenommen werden. Bei hohen Drucken bzw. sehr genauen Messungen wird diese Eigenschaft spürbar. Wasser hat eine Kompressibilität von 0,5 GPa-1, Quecksilber 0.04 GPa-1, Diethylether 1.5 GPa-1, Pentan 2.5 GPa-1. Für Wasser, 100m unterhalb der Oberfläche, führt der hydrostatische Druck (Schwerdruck) (=Dichte*Fallbeschleunigung*Höhe, ρ·g·h) zu einer Volumenverringerung von rd. 0,05%. In Schwebetiefen von 5 cm des Auftriebskörpers bei der hydrostatischen Dichtebestimmung werden 0.2ppm erreicht. Die Schallgeschwindigkeit vs verknüpft Dichte ρ und Kompressibilität Χ n.d.Gl. vs = [Χ·ρ]1/2.(Das Kompressionsmodul K für Festkörper entspricht dem Kehrwert der Kompressibilität und kann aus den Elastizitätskonstanten E-Modul und Poisson-Zahl µ berechnet werden: K = E/(3-6µ).) Während bei Gasen und tropfbaren Flüssigkeiten die Dichte eine Konstante bei jeweiligem Druck (und Temperatur) ist, die sich nach Einwirkung einer Kompression elastisch zurückstellt, findet man bei Festkörpern mitunter andere Verhältnisse. Mit dem Schmieden von Metallen steigt in der Regel die Dichte des Stoffes an. Bei nicht rein-elastischen Materialien, wie etwa dem Polystyrolschaumstoff EPS (Styropor®), ist diese Effekt augenfällig - indem recht einfach bleibende Druckstellen zugefügt werden, die also entsprechend die Dichte erhöhen.
4. Dichte von Mischungen, Gehaltsbestimmung
Seit jeher wird die Dichtemessung zur Gehaltsbestimmung eingesetzt. Für bestimmte Stoffkombinationen, oft wässrige Lösungen z.B. von Zucker, Alkohol (Ethanol) und mit entsprechend eingemessenen Skalen für Milch, Most (Mostgewicht, Öchsle), Batteriesäure (Schwefelsäure in Bleiakkus) etc., werden verbreitet Spindeln eingesetzt (Aräometer, Hydrometer vgl. nächster Abschnitt). In der Regel entspricht die Dichte einer Mischung etwa den Mengenverhältnissen. Die Mischungsdichte kann für zwei Komponenten in einer einfachen Formel ausgedrückt werden. Mit m1, dem Masseanteil einer Komponente mit der Dichte ρ1 und m2, dem Massenanteil der zweiten Komponente und der Dichte ρ2, ergibt sich die Gesamtdichte ρGes der binären Mischung zu: ρGes = (m1+m2)/(m1/ρ1 + m2/ρ2) = (m1+m2)/(V1 +V2)
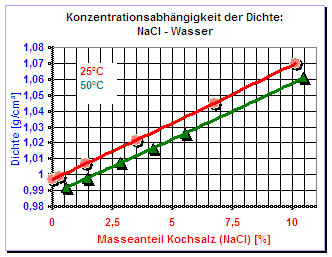
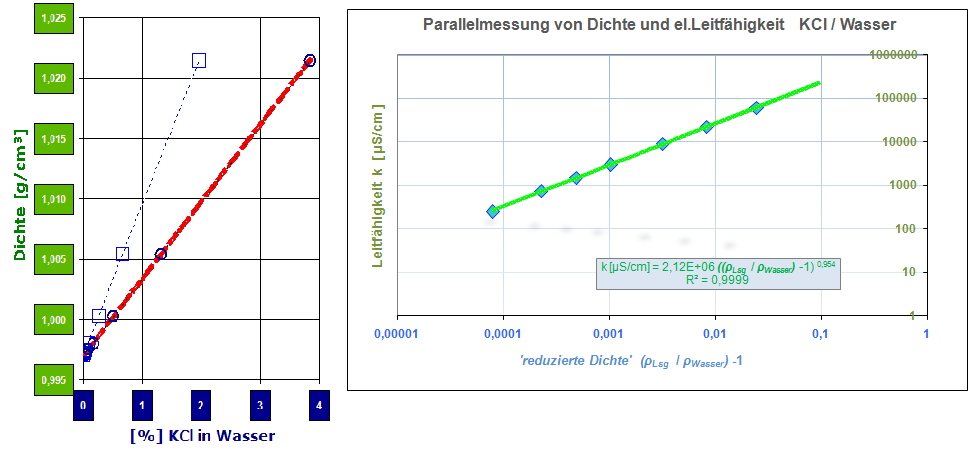
Für in Wasser gelöstes Kochsalz (NaCl) gilt die Beziehung lediglich in der Qualität "π·Daumen", denn die Mischungs- bzw. Lösungsdichte ist bei 10% NaCl bereits um nahezu 1.5% größer, als es sich nach der einfachen Formel ergibt. Im Diagramm (obe n) sind Messdaten zur Dichte von wässrigen Kochsalzlösungen für die Temperaturen 25°C und 50°C abgebildet (Datenherkunft: Rogers, P. S. Z., Pitzer, K. S., J.Phys.Chem Ref. Data, 11, 15 (1982) und aus der ►IMETER Messung ID7277.PDF). Die Abweichung vom linearen Verhalten ist zwar aus der Grafik kaum erkennbar, doch deutlich vorhanden. Mischungen bzw. Lösungen der meisten Flüssigkeiten verhalten sich, wenn genau gemessen wird, ebenso wenig linear. Wobei Mischungen von Essigsäure und Wasser ein extremes Bild zeigen (vgl. Diagramm weiter unten). Wenn Genauigkeit gefordert wird, um über die Dichte definitive Gehaltsbestimmungen anzustellen oder Volumendefekte oder Vergrößerungen (► Hexan/Cyclohexan.pdf) vorhersagen zu können, müssen die Verhältnisse aufgeklärt werden. Dies erfolgt durch exakte Dichtemessungen an mehreren definierten Mischungen und erlaubt dann aus Dichte und Mischungsverhältnissen die Aufstellung einer Kalibrierfunktion. Die folgende Gleichung führt einen spezifischen Faktor in die obige Idealgleichung ein, den MischungskoeffizientenΦ12 : ρGes = (m1+m2) / (m1/(ρ1·Φ12) + m2/ρ2) Der Mischungskoeffizienten Φ12 :ist allerdings eine Funktion des Mischungsverhältnisses, der aus einer Konzentrationskalibrierung bestimmt wird. Für das Beispiel Kochsalz-Wasser wurde eine entsprechende Messung durchgeführt. Diese liefert für den Koeffizienten bei 25°C die Bestimmungsgleichung: Φ12 = 0,4601860 +0,8550176·ρGes -0,3144906·ρGes² In den Fällen, bei welchen die Konzentrationsbestimmung aus Dichtemessung erfolgen soll, kann auch eine einfachere Formulierung eingesetzt werden: Bzw. um die Dichte als Funktion der Konzentration vorherzusagen, kann die aus den Messdaten ermittelte Gleichung ρ [g/cm³] = ƒ(c[%])= 0,9971057 +6,96858E-3·(c) +2,03622E-5·(c)² (±0,0001g/cm³) angewendet werden. Die Gleichungen gelten für den durchmessenen Konzentrationsbereich zwischn 0,0138 bis 10,1% bzw. für Mischungsdichten zwischen 0,997171 bis 1,069934g/cm³; IMETER erzeugt diese Zusammenhänge in einer Konzentrationsmessung automatisch (vgl.►IMETER Messung IDN°7277.pdf). Konzentrationsbestimmungen an Mischungen aus drei Komponenten (ternäre Mischungen) sind auch per Dichtemessung möglich. Beispielsweise könnten die Bestandteile Zucker, Wasser und Ethanol bei alkoholischer Gärung oder Glycerin, Propylenglycol und Wasser als Liquid für EZigaretten in weiten Bereichen bestimmt werden. Dafür wären jedoch zwei Dichtemessungen erfordedrlich. Die Messungen müssen bei verschiedenen Temperaturen erfolgen - und so kann für die Gehaltsbestimmung das entsprechende Gleichungssystem gelöst werden. Entsprechend können Viskosität und Oberflächenspannung, ggf. noch mit deren Temperaturkoeffizienten, herangezogen werden, um die Bestandteile höherer Mischungen physikalisch zu ermitteln.
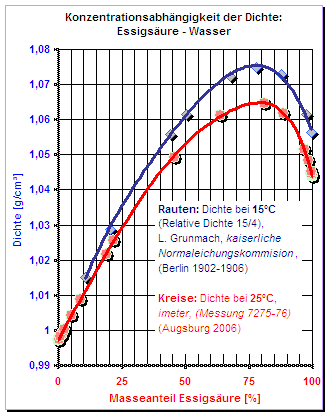
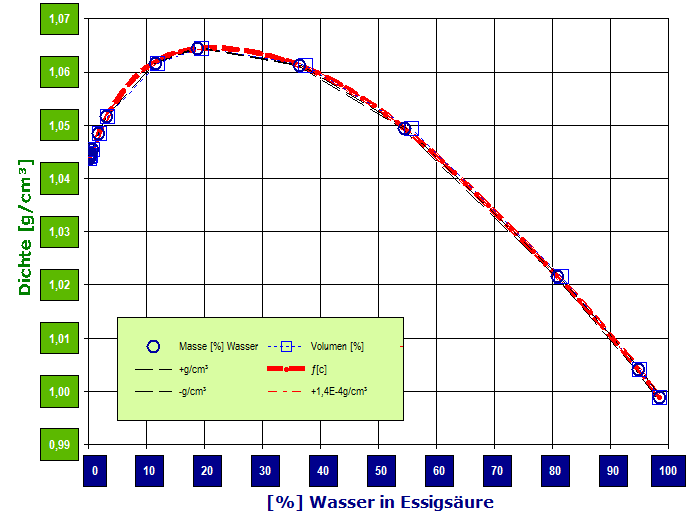
Im Diagramm (Abb.8) wird die Ausnahme der Regel gezeigt: Mischungen aus Essigsäure und Wasser. Bei der Dichte über 1.04g/cm³ können einem Dichtewert zwei unterschiedliche Konzentrationen zugeordnet werden (vgl. ►Messung IDN°7575.pdf,►Messung IDN°7576.pdf ). (Die Ursache für das anomale Verhalten wird deutlich, wenn die Masse% in Mol% umgerechnet wird. Beim molaren Verhältnis 1:1 – bei ca.70% Essigsäure – tritt das Dichtemaximum auf. Die dichteste Packung entspricht dem 1:1 Molekülverhältnis. --- Ein kleiner Zaubertrick: man nimmt ein durchsichtiges Gefäß, das in der Mitte mit einer Trennwand geteilt ist, gibt in die eine Hälfte Essigsäure und in die andere die gleiche Menge 50%igen Essig und in beiden Abteilen ist eine Menge z.B. SAN-Polymergranulat [oder ein anderer Stoff der Dichte von etwa 1.05g/cm³, dem die Säure nichts ausmacht]. Das Granulat liegt in den Gefäßteilen am Boden, da die Dichte des Feststoffs größer ist. Dann zieht man die Trennwand heraus und das Granulat beginnt aufzuschwimmen). Der Essig-Wasser-Sonderfall ist messtechnisch zur Sensoren- und Messapparateprüfung interessant. Denn für ein und dieselbe Dichte, z.B. 1.05g/cm³ (25°C), gibt es zwei unterschiedliche Konzentrationen: Oberflächenspannungen und Viskositäten. So können entsprechende Anzeigegeräte und deren Querempfindlichkeiten zur Dichte geprüft werden - und umgekehrt. Die Dichte ist, wenn sie genau bestimmt wird, für nahezu alle binären Mischungen ein hochexaktes Konzentrationsmaß. Andere Methoden, chromatographische oder spektroskopische, erreichen bei Weitem nicht die Exaktheit, die per Dichtemessung möglich ist. Um Konzentrationskalibrierungen richtig durchführen zu können, sind Bestimmungsmethoden erforderlich, die keine Querempfindlichkeit zu Oberflächenspannung und Viskosität aufweisen, denn diese Eigenschaften ändern sich ebenfalls.
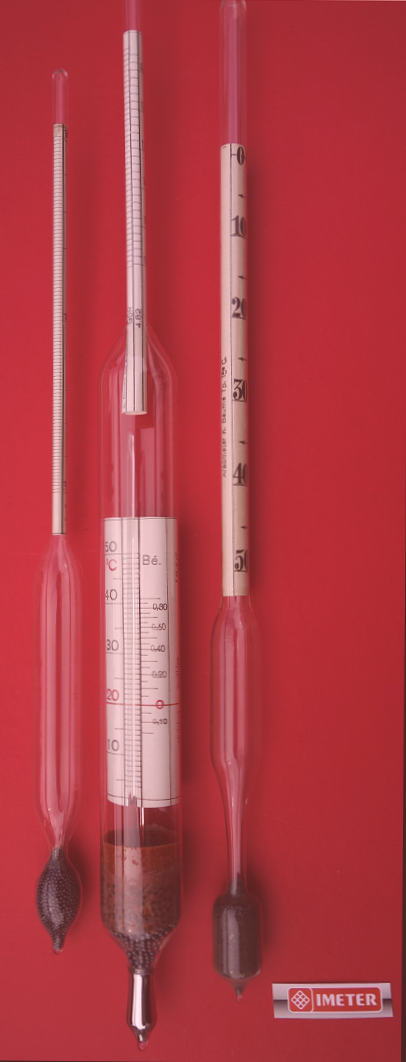
5. Dichte- BestimmungsmethodenMessgeräte - Messvorrichtungen - MessverfahrenMessgeräte für die Dichte werden als Dichtemessgeräte, manchmal als Densimeter bezeichnet. Die Dichtemessung mit einem Densitometer jedoch betrifft z.B. die Schwärzung und Farbdichte - also eine andere Dichteart. Zur Bestimmung der Masse-Dichte sind eine Reihe von Geräten und Methoden gebräuchlich: Aräometer, Pyknometer, hydrostatische Wägung, das Schwingungsmessgerät nebst weniger Gebräuchlichem wie dem Schwebeverfahren und der Dichtegradientensäule, die insbesondere für Festkörper verwendet werden. 5.1. Aräometer (Spindel, Senkspindel, Senkwaage, Hydrometer)Das wahrscheinlich in der Antike schon bekannte Aräometer wurde 1670 von Roberval (wieder-)erfunden. Heutzutage handelt es sich dabei meist um einen luftgefüllten Glashohlkörper, dessen unteres Ende durch eine gewisse Menge aus Bleischrot, Sand oder Quecksilber beschwert ist. Oben läuft der Hohlkörper in einem schmalen, zylindrischen Hals aus, auf dem eine eingemessene Skala angebracht ist. Je tiefer das Aräometer in die Flüssigkeit eintaucht, desto kleiner ist die Dichte. Im allgemeinen benutzt man in Labors einen Satz von 14 Aräometern, um Dichten zwischen 0.630 und 2.000 g/cm3 zu messen (Messspanne je Spindel 0.1 g/cm3). Die Dichte wird mithilfe eines Standzylinders, in den die Flüssigkeit eingefüllt wird, gemessen. Das Aräometer muss beim Ablesen frei und bewegungslos schweben und die Temperatur muss der Bezugstemperatur des Aräometers entsprechen. Die Messunsicherheit beträgt je nach Spindel typischerweise 1·10-3 g/cm³ bis bestenfalls 1·10-4 g/cm³ bei sehr speziellen Ausführungen. Neben den Spezialformen, die auf die hohe, mittlere oder niedrige Oberflächenspannung des Messgutes eingestellt sind und die Durchsichtig- oder Undurchsichtigkeit berücksichtigen, gibt es auch Spezialaräometer wie Alkoholometer, Milcharäometer und Saccharimeter, die durch eine bestimmte Eichung z.B. ein direktes Ablesen des Prozentgehaltes an der Skala ermöglichen. Außer der Teilung der Skala nach Dichtewerten sind noch andere Skalen in Gebrauch. Es gibt die Unterteilung in Grade Baumé, Cartier, Beck, Brix, Balling, Gay-Lussac und Twaddle. DIN 12790, ISO 387 Aräometer; allgemeine Bestimmungen
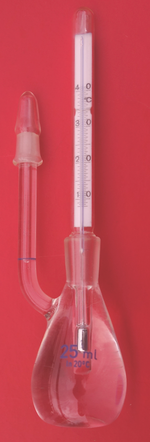
5.2. Pyknometer (Volumenwägung, Density Bottle)
|
7. IMETER - die Ergänzungen zur klassischen Messtechnik |
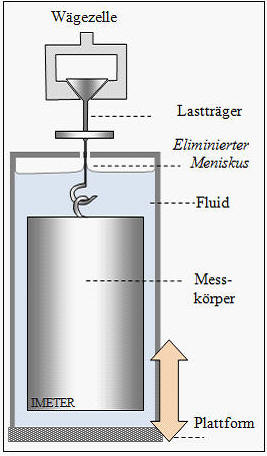
7.1. Meniskuseliminierung:
Die Meniskus-Eliminierung ist der Vorgang, in dem der Messfehler bei der hydrostatischen Dichtemessung behoben wird. Der in statischen Messungen unbehebbare Fehler besteht darin, dass der Einfluss des Flüssigkeits-Meniskus durch die Aufhängung des Messkörpers nicht genau bestimmbar ist. Jedoch in einem Verfahren, d.h. einem Handhabungsprozess, kann dieses allgemeine Problem der Phasengrenzen aufgelöst werden.
IMETER bietet zwei Varianten zur Lösung:
1. Explizite Vor- oder Nachbestimmung der Korrektur:
Das Aufhängungsmittel wird austariert, dann bis zu einer Marke an der Suspension in die Flüssigkeit eingeführt und um eine definierte Strecke zurückgezogen (um einen rückwärtigen Kontaktwinkel in der Phasengrenze zu erzeugen). Die hier auftretende Gewichtskraft wird bestimmt. Sie beinhaltet den Auftrieb der Halterung und die Meniskuskraft in der Messposition. Diese Korrekturkraft wird vom Kraftmesswert bei der Feststoff- bzw. Flüssigkeits- Auftriebsmessung abgezogen.
2. Implizite Auslöschung ("Die Meniskuseliminierung"):
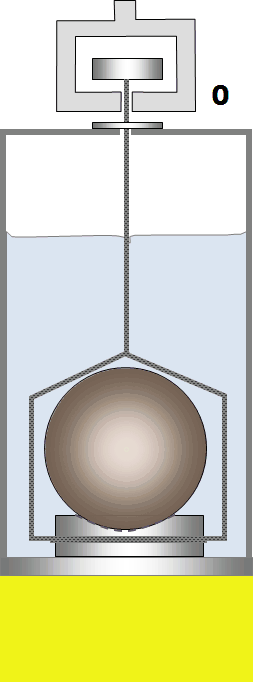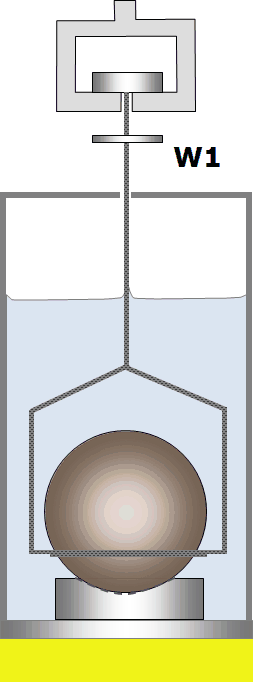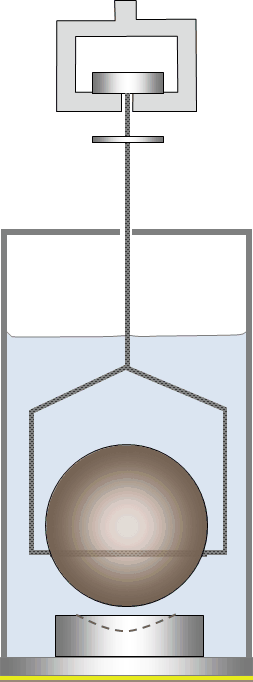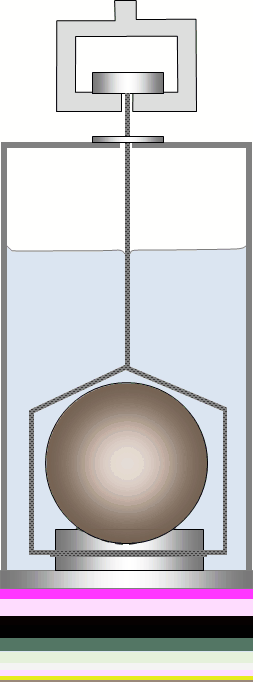
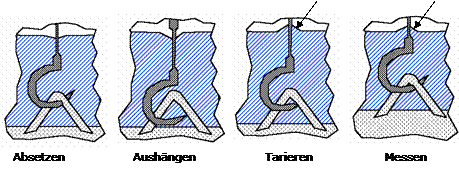
Mess- oder Prüfkörper oder Probenbehälter werden untergetaucht, auf einem Boden abgestellt oder ausgehängt bzw. aus dem Haken gehoben, indem das Gefäß durch die Positioniervorrichtung angehoben wird. Die Bildsequenz unten zeigt das Prinzip. Tarieren und Messen (3. und 4. Bild) findet mit gleichen, rückwärtigen Kontaktwinkeln statt. Das Drahtstück, das beim Messen gegenüber dem Tarieren austaucht, wird natürlich berücksichtigt. Die Dichtemessung ist in diesem Fall eine Differenzmessung.
Mit dem Tarieren werden noch andere Störungen eliminiert, wie die Drift des Nullpunktes der Wägeeinheit, schleichende Verschmutzung oder Kondensation von Flüssigkeitsdampf an der Aufhängung und auch der Effekt durch variable Flüssigkeitsniveaus bzw. Eintauchtiefen.
Welches Verfahren zum Einsatz kommen soll, richtet sich nach den jeweiligen praktischen Erfordernissen. Das explizite Verfahren kann für rasche Einzelmessungen mit geringeren Präzisionsansprüchen geeignet sein, Verfahren 2 für Messungen mit höherem Präzisionsanspruch sowie für länger währende Messungen und Monitorings.
Erläuterung zu "ohne systematische Fehler"
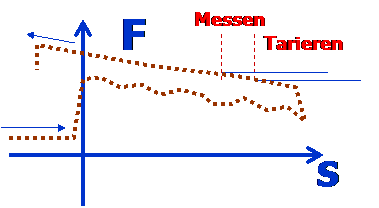
Der Fehler der Auftriebskraftmessung, wie er durch den Meniskus nach traditioneller Technik auftritt, wird in dem Diagramm unten gezeigt; er entspricht darin dem Kraftsprung insgesamt. Mit der neuen Technik wird der Sprung zunächst verkleinert und schließlich ganz ausgelöscht:
Zur Skizze: Wenn man einen benetzbaren Draht einer Wasseroberfläche annähert, dann springt am Berührpunkt die Flüssigkeit diesen an – es entsteht ein Meniskus, der am Draht zieht. Taucht man den Draht weiter ein, dann gleitet das Wasser etwas unregelmäßig über die Drahtoberfläche; mal wiegt dieser Meniskus etwas mehr, mal weniger. Denn der Vorrückkontaktwinkel ist auf nicht-vorbenetzter Oberfläche oft ungleichmäßig. Der Auftrieb, der auf den Draht wirkt, nimmt mit zunehmender Eintauchtiefe zu. Dadurch fällt die Kraft letztlich kontinuierlich ab (die Kurve geht nach unten, denn der Volumenauftrieb entlastet das Anfangsgewicht). Zieht man den Draht heraus - die Kurve kehrt um - und es fließt das Wasser von der vorbenetzten Drahtfläche ab, ist der Kraftverlauf wesentlich gleichmäßiger. Für die Dichtemessung ist nun der kleine Abschnitt ΔSk , zwischen Tarieren und Messen, von Einfluss. Dies entspricht, übertragen, dem Stadium, in dem der Messkörper abgestellt ist (mit rückwärtigem Kontaktwinkel am Draht) und der Messposition, in welcher der Messkörper wieder anhängt und der Auftrieb gewogen wird.
Nun, mit dem Drahtquerschnitt, der Bewegungsstrecke und der Dichte (in Rekursion ermittelt) ist der kleine Beitrag ΔFk vollständig bestimmt. Diese Kraft wird berechnet und zur Korrektur der Auftriebskraft des Messkörpers verwendet. Der Fehler ist damit behoben. Es bleibt für die Ausgestaltung im konkreten Setup einer Messapparatur frei, inwieweit die gleichwohl durch die Doppelwägung entstehende Unsicherheit reduziert wird. Grundsätzlich sollte aber der Draht so dünn, so glatt und so gleichmäßig wie möglich und die Phasengrenze der Flüssigkeit homogen sein.
7.2 Mittelwerte
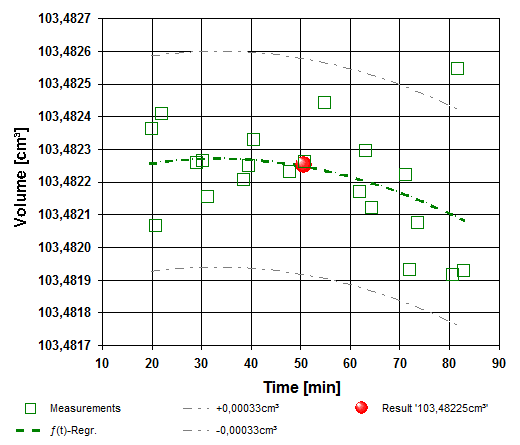
Bei einem einzelnen Messwert kann besonders bei einer unbekanten Probe die Messunsicherheit aus den Daten der beteiligten Sensoren und der Qualitätseinschätzung zur Temperierung abgeleitet werden. Ob die Messung durch einen Fehler beeinträchtigt ist, kann sich aus einem einzelnen Messwert nicht ableiten lassen. - IMETER bietet neben der richtigen Verfahrensweise und Ausrüstung auch die Softwaretechnischen und ideellen Hilfsmittel für die Steigerung von Qualität und Sicherheit an. Die Eliminierung von Meniskus und Zeiteffekten ist ein Teil, die Möglichkeit der Messung in unabhängigen Mittelwerten ein anderer. Unabhängige Mittelwerte werden gemessen, indem der Messprozess mitsamt der Meniskuseliminierung wiederholt wird. Die Software unterstützt dies direkt und übrigens auch unter Variation der Positionen, der Temperatur, der Probensubstanz etc..
Mittelwert und Standardabweichung sind die zentralen Eingangsgrößen zur Beurteilung der Qualität einer Messung. Die Leistungsdaten der Sensoren selbst sind unbedeutend, wenn die Probe aufgrund ihrer Konstitution (Mehrphasigkeit, Inhomogenität, Stabilität) nicht eindeutig vorliegt. Fehler z.B. durch Luftblasen, eine unvollständige Temperierung oder Zufälligkeiten fallen mit der Beobachtung mehrerer Messwerte aus dem Verlauf der Einzelwerte auf.
In Wiederholungsmessungen möchte man für die richtige Statistik, die Wiederholstandardabweichung und die Findung des wahren Wertes, ja genau nicht die Schwankungsbreite der Bedienvariationen der Prüfer sondern die der Messung haben. Das wird so erledigt. In der Prozess-Steuerung kann genauso, wie das Aushängen der Messkörpersuspension erfolgt, die Auflage eines (weiteren) Justiergewichtes eingerichtet werden. Es kann auch ein Massekomparator eingesetzt werden.
7.3 Alternierende Flüssigkeits und Feststoffdichtemessung
Eine datentechnische Automation ermöglicht bei der Feststoffdichtemessung einen weiteren Effekt für die Erhöhung von Qualität und Richtigkeit. Wenn Flüssigkeitsdiche und Feststoffdichte evtl abwechselnd gemessen werden, dann wird die mit einem Messkörper gemessene Flüssigkeitsdichte (sie ist ja für die Auftriebsmessung der Feststoffprobe maßgeblich) für die Feststoffdichtemessung als Massstab verwendet. Es muss also nicht eine bestimmte Flüssigkeit mit vorbekannter Dichte eingesetzt werden - jede beliebige Flüssigkeit kann so verwendet werden. Und wenn die Feststoffprobe mit der Flüssigkeit reagiert, wird dies an der Änderung der Flüssigkeitsdichte erkennbar. Im Prinzip findet durch dieses Verfahren die Übertragung der Kalibrierung, d.h. der Normaleigenschaft des Flüssigkeitsdichte-Messnormals auf die Probe statt. Deren Dichte ist dann nahezu so genau bestimmt, wie die des Normals. Es handelt sich bei diesem oft im Hintergrund ablaufenden Verfahren, um eine automatische Rückführung auf das Messnormal, aus dem sich die Messkörpereigenschaft herleitet. Der Messkörper sollte an ein Normal angeschlossen sein.
7.4 IMETER Framework
IMETER ist ein Werkzeug, das den Zugriff auf die Stoffeigenschaft „Dichte“ durch allgemeine und universelle Anwendung der hydrostatischen Methode für die Dichtebestimmungen und Dilatometrie an flüssigen und festen Stoffen zur Verfügung stellt.
- Es werden alle effektiven Einflussgrößen berücksichtigt.
- Die Einflussgrößen können mit dem MessSystem bestimmt werden (Luftdichte, Absolute Dichte).
- Dichte und Ausdehnungskoeffizienten können zusammen in einer Messung bestimmt werden.
- Die Ergebnisse sind rückführbar auf gesicherte Normale.
- Die Ergebnisausgabe erfolgt in Echtzeit und kann zur Online-Regelung verwendet werden
- Da die Prozesssteuerung einen Zugriff auf Erfahrungswerte bietet, können auch bestimmte Dichten eingeregelt werden (Dosierung, Temperatur, Druck).
Zum Erreichen des Optimums im Spannungsfeld von Aufwand und Präzision stehen innerhalb der frei modellierbaren Abläufe verschiedene Arbeitsmodi zur Verfügung. So können Zubehör und Arbeitsabläufe auf die Fragestellung genau angepasst werden.
- Messprogrammkonzept - (Messablaufvarianten, Dialogelemente zur Unterstützung des Prüfers etc.).
- Meniskuskraft-Korrektur durch experimentell vor- und/oder nach-bestimmbare Beträge.
- Meniskuskraft-Eliminierung durch ein spezielles Verfahren (ohne systematische Fehler!).
- Driftkompensation und Justierung während der Messung (...auch auf Dauer genauer).
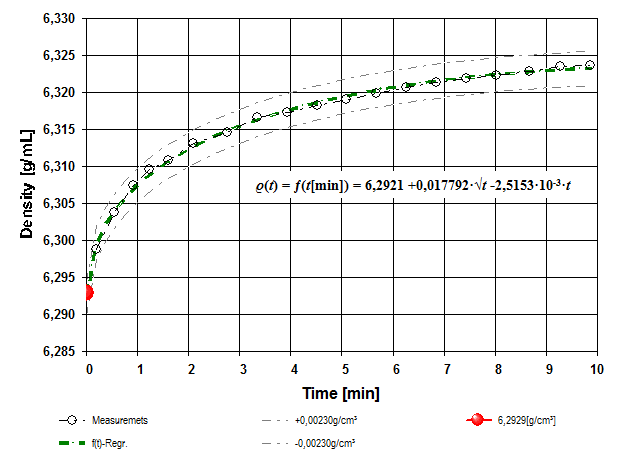
Für Anwendungen der Flüssigkeitsdichtemessung kann das Absolut-Verfahren angewendet werden. Die Viskosität ist ohne prinzipiellen Einfluss, wie auch optische, elektrische und - unter Einschränkungen - magnetische Eigenschaften; die Probe kann instabil sein und als Emulsion, Suspension oder Gel vorliegen. Aus Dichtewerten kann die Kinetik von Vorgängen erhalten werden, die die Dichte der flüssigen Phase selbst oder die Messung der Dichte beeinflussen, wie etwa Temperaturangleichung, Sedimentation, Koagulation, Ausfällung, Kristallisation, Aufrahmung, Auflösung oder allgemein Konzentrationsänderung und Stoffumsatz. Darüberhinaus bietet die IMETER-Dichtemessung auch die Möglichkeit zur Kalibrierung der Temperaturmessung im Millikelvinbereich.
IMETER ist ein formales und freies System, welches beachtliche Teile der Eigenschaftsmessung und Werkstoffprüfung umfasst. Anwender haben sogar die Freiheit, selbst Zubehör und Handhabungen (z.B.) der Dichtemessung so einzustellen, wie Zwecke es im Wandel der Zeit und der Aufgaben erfordern. Sprachelemente der Steuerung und technische Einrichtungen des Gerätes erlauben quasi jede denkbare Anwendung in Labor oder Betrieb mit geringem Aufwand auszurüsten. Die automatische Nullpunktnachführung, die Justierbarkeit während längerer Messungen, die Verhinderung systematischer Fehler (Meniskuskraft-Eliminierung) sowie die Unabhängigkeit von der Temperatur und die automatische Ermittlung des individuellen Messfehlers – sich ergebend aus Auflösung, Messkörperdaten, Messdaten und Probeneigenschaften etc. – sind Merkmale der Technik, die für eine grundlegende und nachhaltige Lösung stehen.
8. Formeln zur hydrostatischen Dichtemessung
Die Definitionsgleichung der Dichte lautet :
ρ = m / V
Die einfache Formel drückt als Dichte das Verhältnis von Masse zu Volumen bzw. die Konzentration von Masse in einem Volumen aus. Die hydrostatische Dichtebestimmung besteht im Prinzip aus zwei verschiedenen Messungen. Der Messung der Masse und die Messung des Volumens; letztere ist im eigentlichen Sinne die hydrostatische Messung.
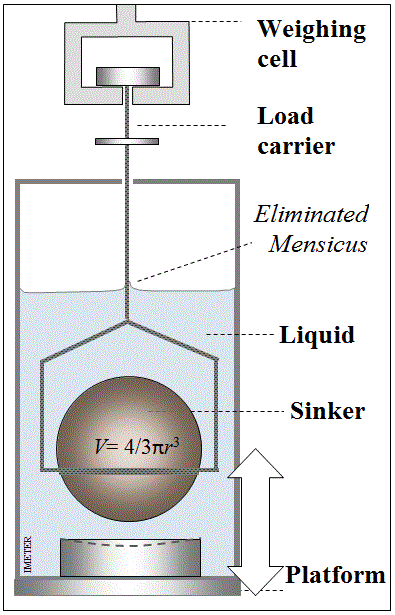
Das nachfolgende Bild zeigt die fundamentalen Verhältnisse bei der hydrostatischen Wägung zur Bestimmung der Dichte einer Flüssigkeit:
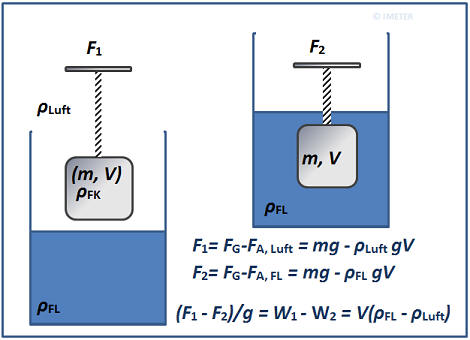
Z.B. mit einer Federwaage kann man die Gewichtskraft F1 bei Wägung an der Luft und F2 bei der getauchten Wägung bestimmen. Wägewerte, W, die an üblichen Waagen abgelesen werden, sind Gewichtskräfte. Mit dem Ortsfaktor g (Fallbeschleunigung) erhält man die jeweilige Gewichtskraft der Masse (FG=m·g). Das Volumen der Masse führt wie in der Flüssigkeit so auch in der Luft zu einer Auftriebskraft (FA, Luft = ρLuft·V·g). Über die oben gezeigten Gleichungen für F1 und F2 liefert Gleichung I eine korrekte Formulierung für die Bestimmung der Flüssigkeitsdichte:
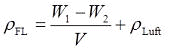
(Gl. I)
Hier muss die Masse des Auftriebskörpers (Festkörpers, Messkörpers) nicht bestimmt sein. Mit V = ΔW / Δρ ist bei bekannter Flüssigkeitsdichte auch die unmittelbare Volumenbestimmung eines Körpers möglich.
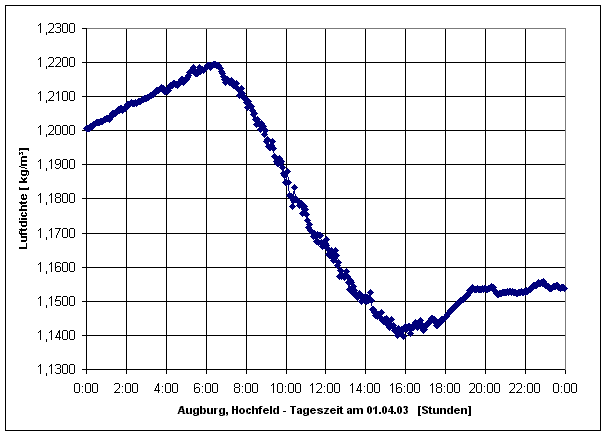
Soll die Dichte über längere Zeit hinweg - und exakt - gemessen werden, so sind W1 und W2 nicht mehr miteinander vergleichbar, da sich die Luftdichte geändert haben kann (vgl. Diagramm weiter oben zur Luftdichteschwankung). Außerdem ist es in der Praxis unnötig mühsam und fehleranfällig, den Messkörper jedesmal vorher zu wiegen. Besser ist es, man hat Masse und Volumen des Körpers und kann jeweils den Wägewert zur jeweiligen Luftdichte berechnen. Auch ist es schwierig in der Gleichung I notwendige Korrekturen etwa durch die Aufhängung, die Kompressibilität und bei Temperaturänderung unterzubringen.
Wie kommt man an die Masse? Auch wenn elektronische Waagen mg/g/kg -Masseeinheiten anzeigen - eine Wägung liefert einen Wägewert. Nur im Vakuum sind Schwere und Masse äquivalent. Die Balkenwaage ist eine sehr geeignete Einrichtung, um auch hier das Grundsätzliche zu klären: Die Balkenwaage ist im Gleichgewicht, wenn auf der linken und rechten Seite die gleiche Gewichtskraft wirkt; dazu die folgende Skizze mit Gleichung:
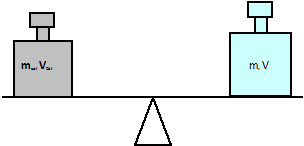
mcal·g – ρLuft·Vcal·g = m·g - ρLuft·V·g (Gl. IIa)
Im Gleichgewicht ist die Kraft auf der linken Seite des Wägebalkens (F=m·g ), unter Wirkung des Luftauftriebs (Fa= ρLuft·V·g), gleich der Kraft rechts. In der Gleichung IIb wird g gekürzt, das Körpervolumen V durch die Dichte ersetzt (V=m / ρ) und die Masse vor die Klammer gezogen:
mcal ( 1 – ρLuft /ρcal) = m (1 - ρLuft/ρ) (Gl. IIb)
"ρLuft" steht allgemein für Dichte des Mediums in dem der Vergleich stattfindet. Im Vakuum fällt der Auftriebsterm natürlich weg und Massen sind mit ihren Gewichtskräften über g zahlengleich. Die Fallbeschleunigung g ist dabei genaugenommen nur dann gleich, wenn der Schwerpunkt beider Körper auf gleicher Höhe ist. Die Mediumdichte (ρLuft) muss natürlich auch auf beiden Seiten gleich sein.
Eine allgemeine Formulierung findet sich in der Literatur [z.B. Lit.87, Kap.13]:
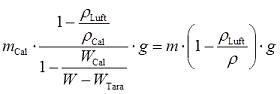 (Gl. IIc)
(Gl. IIc)(W ist dann gleich dem Zahlenwert des konventionellen Wägewerts, wenn Wcal ≡ mcal und ρcal =8,000 g/cm³, bei 20°C und ρLuft =1.2 kg/m³)
In Gleichung IIc steht der Kalibrierstandard mit dem Gewicht Wcal, der Masse mcal, der Dichte ρcal mit dem Gewicht W, der Masse m und der Dichte ρ der Objektwägung im Gleichgewicht. WTara ist der Wägewert ohne Objektauflage. Wenn Wcal=mcal und der Leer-Wägewert WTara auf Null gesetzt ist, ergeben sich daraus ebenfalls die übersichlicheren Gl. III und IV:
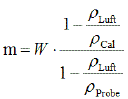 und
und 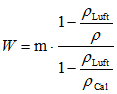
Die Gleichungen erlauben die Umrechung zwischen Masse- und Wägewertangaben. Um die Masse (m), d.h. die wahre Masse angeben zu können, müssen neben dem Wägewert und der Dichte des Wägegutes (ρ d.h. ρFK) auch die Luftdichte (ρLuft) und die Dichte des Kalbriernormals (ρcal) der Waage bekannt sein. Der einzusetzende Dichtewert ρFK ist bei Feststoffen die Rohdichte, die inklusive des für das Medium (Luft) unzugänglichen Porenvolumens bestimmt ist.
|
(Gl. V)
(Gl. VI)
(Gl. VII)
(Gl. VIII)
|
Auf den ersten Blick erscheinen die Formeln, links, etwas umständlich. Dies ist auch dadurch bedingt, dass die Luftdichte und deren Veränderlichkeit berücksichtigt werden kann. Der Wägewert W1* muss nicht als solcher jeweils bestimmt werden (das wäre umständlich bzw. unmöglich bei Inline/-Monitoring-Messungen und anderen längerwährenden Beobachtungen). Der Wägewert kann jederzeit aus einer hinterlegten Masse mit je aktuellen Luftdichtedaten berechnet werden. Genau so, wie Volumen und Dichte von Messkörpern in Druck-/ Temperaturabhängigkeit parallel zu jeweilgen Umständen durch die formelmäßigen Zusammenhänge bestimmt werden. ρFL Dichte der Flüssigkeit
|